Интегральный метод определения размера главного пользования лесом
Рационально установленный размер ежегодной основной рубки в первую очередь зависит от наличия в хозяйстве спелого леса. Он обязан определяться с таким расчетом, дабы в рубку поступал лишь спелый лес. Наряду с этим пользование лесом должно быть постоянным, т.е. с каждым годом повторяющимся, и вместе с тем довольно равномерным.
Дабы установить размер пользования лесом, удовлетворяющий этим условиям, нужно располагать данными распределения древостоев по возрасту и в один момент учитывать интенсивность накопления в хозяйстве спелого леса. Динамика накапливания спелого леса возможно продемонстрирована на особом графике.
На этом графике по оси абсцисс отложены периоды лесопользования, равные 20, 40, 60 годам и т.д. На оси ординат фиксировано наличие спелого леса в отдельные расчетные периоды. Против нулевого деления на оси ординат указано наличие перестойного леса Fnep, т.е. имеющего возраст выше числа лет в обороте рубки.
В приведенных формулах FcP свидетельствует площадь средневозрастных древостоев, отнесенных к классу возраста смежному с приспевающими; F[р — площадь средневозрастных насаждений следующего класса; FMon — площадь молод-няков в смежном классе со средневозрастными насаждениями. Деление древостоев на возрастные категории зависит от оборота рубки.
В отечественных расчетах все древостой, превышающие по возрасту оборот рубки, названы
перестойными Fnep, а относящиеся к классу возраста, верхняя граница которого сходится с числом лет в обороте рубки, спелыми Fcп. Древостой смежного класса отнесены к приспевающим Fnp. Насаждения следующих двух классов возраста названы средневозрастными.
Класс возраста, смежный с приспевающими насаждениями, обозначен через FcP, а следующий — через Fcp.
Точки, характеризующие площади эксплуатационного леса, накопленные за 20, 40, 60, 80 и 100 лет, нанесем на график и соединим отрезками прямых линий. Полученная наряду с этим ломаная линия возможно обращена в плавную кривую, именуемую в математике интегральной. Из конечной точки данной кривой на ось абсцисс опустим перпендикуляр. Так, мы возьмём замкнутый контур, имеющий сходство с трапецией, у которой одна из сторон — кривая линия.
Площадь этого графика характеризует наличие в хозяйстве эксплуатационного леса, накопленного за 100 лет. В течение этого периода без ущерба для лесного хозяйства возможно вырублена накопленная площадь эксплуатационного леса.
Рис. 1. Параболическая криволинейная трапеция
Формула Симпсона решает задачу по определению квадратуры либо площадей трапеций, одна сторона которых ограничивается кривой линией. Нас же интересуют трансформации не площади, а только самой кривой линии, ограничивающей площадь. Исходя из этого мы преобразовали формулу Симпсона, освободившись от множителя, ведущего к квадратуре.
Это удалось сделать методом приравнивания множителя к единице.
Какие конкретно преимущества имеет расчет размера пользования лесом по преобразованной формуле Симпсона? Узнаваемые в лесоустройстве формулы, определяющие размер пользования, исходят из прямолинейного распределения древостоев по возрасту. Следовательно, в базе их лежит предположение, что в пределах расчетного периода древостой имеют равномерное возрастное распределение.
В конечном итоге для того чтобы явления не отмечается. Насаждения, образующие отдельное хозяйство, в большинстве случаев, неравномерно распределены по возрасту. Это распределение характеризуется той либо другой кривой, относящейся к классу парабол.
Параболическое распределение самый полно учитывает формула Симпсона.
При определении по ней средневзвешенной ординаты у, характеризующей в расчетном периоде наличие эксплуатационного леса, в число слагаемых входят начальные и конечные ординаты, но громаднейшую роль играется протяженность промежуточных ординат, входящих в формулу с множителем 4. Такая конструкция формулы и разрешает самый полно учитывать особенности возрастного распределения древостоев каждого хозяйства.
Способы приближенного вычисления интегралов используются при самых узких и важных расчетах. Вследствие этого °ни в полной мере приемлемы для расчета пользования лесом, создаваемого с ограниченной точностью.
В последнее слагаемое этих формул включают площади древостоев высшего класса возраста в площади оборота и пределах рубки всех более ветхих древостоев, если они имеются в данном хозяйстве. Форма кривых, отграничивающих верхнюю сторону трапеций, выясняется различной.
В случае если в хозяйстве преобладает перестойный и спелый лес, то кривая получается выпуклой (рис. 30, а). В истощенных хозяйствах, где преобладают средневозрастные древостой и молодняки, кривая выясняется вогнутой вовнутрь трапеции.
При довольно равномерном распределении древостоев по возрасту кривая трапеций приближается к прямой.
Громаднейшую площадь имеют криволинейные трапеции, характеризующие возрастное распределение с преобладанием высоковозрастного леса.
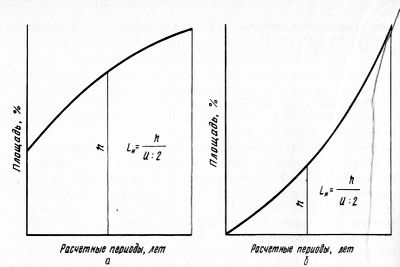
Рис. 2. Криволинейные трапеции распределения древостоев по возрасту:
а — с преобладанием перестойного и спелого леса; б — с преобладанием средневозрастных древостоев и молодняков
Мельчайшей выясняется площадь криволинейных трапеций для хозяйств с преобладанием средневозрастных древостоев и молодняков. Криволинейные трапеции для хозяйств с довольно равномерным распределением древостоев по собственной форме приближаются к прямоугольным треугольникам.
Величина оснований всех трех названных видов криволинейных трапеций однообразна. Она измеряется числом лет в обороте рубки. Высоту криволинейных трапеций характеризует ордината, взятая на середине трапеции.
Протяженность средней ординаты определяет наличие эксплуатационного леса в хозяйстве, которое оно может иметь по истечение периода, равного половине числа лет в обороте рубки.
Рис. 3. Криволинейная трапеция Довольно равномерного распределения древостоев но запасу
отличие новой лесосеки от обычной. Новая лесосека есть комплексной, накапливающей в себе обычную и возрастную лесосеки. Обобщение в один норматив обычной и возрастной лесосек разрешает сохранить хорошие стороны обеих этих лесосек и устранить их недочёты.
Срединная ордината—это интегральное выражение возрастной структуры древостоев, образующих данное хозяйство. В хозяйствах с накопленными запасами высоковозрастного леса срединная ордината имеет громаднейшую величину. Лесососека, определяемая методом деления срединной ординаты на пол-оборота рубки, оказывается большей, чем обычная лесосека.
Срединная ордината криволинейных трапеций, характеризующих хозяйство с преобладанием средневозрастных древостоев и молодняков, имеет мельчайшую величину. У данной трапеции кривая (верхняя) сторона вогнута вовнутрь трапеции. В следствии деления укороченной ординаты на тот же делитель приобретаем меньшую лесосеку, чем обычная.
В хозяйствах с равномерным возрастным распределением древостоев все три вида лесосек (обычная, возрастная и новая комплексная) получаются родными друг к другу.
При равномерном возрастном распределении древостоев криволинейная трапеция обращается в фигуру, близкую к прямоугольному треугольнику. В последний возможно вписать последовательность аналогичных треугольников, у которых отношение длины одного катета к длине другого, либо отношение длины ординаты к абсциссе — величина постоянная. Все три вида лесосек (новая комплексная, обычная и возрастная) находят делением соответствующей ординаты на абсциссу.
Потому, что в разглядываемых прямоугольных треугольниках отношение одного катета к второму —одинаковая величина, то соответственно этому все три вида названных лесосек равны между собой.
Новая комплексная лесосека взята методом интегрирования площадей криволинейных трапеций, характеризующих распределение древостоев по возрасту. Отысканная наряду с этим протяженность срединной ординаты есть интегральным выражением возрастного распределения древостоев. Она аккумулирует в себе все особенности возрастного распределения древостоев.
Размер это срединной ординаты обусловливает величину нового вида леср-секи. Все изложенное и послужило основанием новую лесосеку назвать интегральной. Эта лесосека синтезирует обычную и возрастную лесосеки.
Регулирование размера рубки леса величиной интегральной лесосеки снабжает: непрерывность лесопользования, относительную его равномерность, пользование лишь спелым лесом, согласование размера рубок с наличием спелого и перестойного постепенное улучшение и леса возрастного строения леса.
При построении криволинейных трапеций появляется вопрос о том, за какой период нужно учитывать динамику поспевания леса. Тут смогут быть различные ответы, но все они зависят от распределения насаждений по возрасту. В случае если древостой, входящие в состав хозяйства, имеют равномерное распределение по возрасту, то построение криволинейной трапеции, характеризующей динамику поспевания леса, может ограничиться отрезком времени в 30—40 лет.
В истощенных хозяйствах с недочётом спелых древостоев выравнивание пользования лесом должно осуществляться за счет ближайших и более отдаленных резервов, т.е. приспевающего и средневозрастного леса. В подобном положении выясняются хозяйства с накопленными запасами спелых и перестойных древостоев. При выравнивании пользования лесом избыток перестойного и спелого леса в них нельзя реализовать в маленький период.
Поднявшись на противоположный путь, мы неизбежно пришли бы к резкой неравномерности в пользовании лесом. Дабы этого избежать, в базу расчетов должна быть положена динамика поспевания насаждений за долгий период. В этом случае вырубка имеющегося спелого и перестойного леса растягивается на более долгое время.
Так, в отношении истощенных хозяйств и хозяйств с преобладанием перестойных и спелых древостоев для верного определения размера пользования нужен учет динамики поспевания леса за долгий период, в собственном пределе равный числу лет в обороте рубки.
В средней полосе СССР преобладают насаждения, относящиеся ко II и III классам бонитета. В таких условиях произрастания для хвойных пород значительно чаще устанавливают обороты рубки длительностью 100 лет. В отдельных географических территориях страны условия местопроизрастания, обусловливающие скорость роста леса, обширно варьируют.
Имея это в виду, применительно к изложенному выше способу выведены формулы для определения расчетной лесосеки при оборотах рубки, начиная с 70 лет и заканчивая 140 годами.
Выведенные формулы говорят о том, что величина размера пользования в основном зависит от наличия в хозяйстве спелого, приспевающего и средневозрастного леса. Площадь молодняков несущественно воздействует на размер годичной рубки.
В то время, когда в базу расчетов положена формула Симпсона, громаднейшее значение придается величине, занимающей срединное значение, потому, что она входит в формулу в учетверенном виде (срединная ордината в формуле Симпсона имеет коэффициент 4). Эта особенность формулы, определяющая параметры интегральной кривой, разрешает машинально приводить размер годичной рубки в соответствие с возрастным распределением древостоев.
В случае дефицита в хозяйстве спелого и приспевающего леса срединная ордината параболитической трапеции будет иметь малого величину, в связи с чем и размер пользования лесом быстро снизится. В хозяйствах, где преобладают спелые и приспевающие древостой, срединная ордината будет намного больше, исходя из этого в них значительно возрастёт размер пользования лесом. Многократные испытания результатов расчета разрешают сделать вывод, что приближенное интегрирование, осуществленное применительно к формуле Симпсона, разрешило возможность вывести новые формулы, в равной мере пригодные для применения в хозяйствах с разнообразным распределением древостоев по возрасту.
Интегральный способ определения расчетной лесосеки есть комплексным решением проблемы, фиксирующим идею обычной лесосек и лесосеки по возрасту. Он сочетает преимущества этих двух видов лесосек и вместе с тем ликвидирует недочёты.
Главное преимущество интегрального способа содержится в том, что он определяет большую вероятную расчетную лесосеку, в большинстве случаев, обеспеченную спелым лесом в течении всего оборота рубки.
Отдавая должное классическим способам определения расчетной лесосеки, надлежит иметь в виду, что интегральная лесосека есть следующим шагом на пути совершенствования методики определения пользования лесом.
Выше изложен множество способов, разрешающих выяснить размер главного пользования лесом.
Проделав соответствующие расчеты, по всем рассмотренным методам, возьмём конечные результаты, имеющие те либо иные расхождения. Вследствие этого появляется вопрос: какую из взятых лесосек принять за расчетную? На данный вопрос не представляется вероятным дать однозначный ответ.
При довольно равномерном распределении древостоев по возрасту и верном установлении оборотов рубки в качестве расчетной возможно принята обычная лесосека.
Значительно чаще в устраиваемом лесу обнаруживается неравномерное распределение по возрасту. В таких случаях при расчете размера главного пользования лесом важное значение имеет
всесторонний учет возрастной структуры древостоев, образующих отдельное хозяйство.
Возрастное распределение более полно учитывается второй возрастной лесосекой, лесосекой Самгина и интегральной лесосекой. Последние являются лесосеками комплексными, накапливающими в себе обычную и возрастную лесосеку. Интегральная лесосека опирается на наличие в хозяйстве спелого леса и самый полно учитывает динамику поспевания леса. Она создана для различных оборотов рубок, начиная с 70 и до 140 лет.
Все это дает основание вычислять, что она снабжает самые надёжные результаты расчетов.
Для решения многих технических и экономических задач на данный момент обширно употребляется линейное программирование. При помощи его решают задачи, названные экстремальными. Их сущность содержится в нахождении большого иди минимального значения некоей величины (целевой функции) при соблюдении заданных условий, ограничивающих искомый итог.
Расчет лесопользования возможно отнести к ответу для того чтобы рода задач. В конечном счете он сводится к нахождению большого значения вероятного ежегодного размера рубки леса, выполняя наряду с этим обязательность постоянного, неистощительного лесопользования, правила лесоводства и кое-какие экономические условия.
Для определения размера пользования лесом способ линейного программирования применили В. Д. Волков и Д. Н. Дудин. В базу собственных расчетов они положили последовательность лесохозяйственных условий, сводящихся к следующему.
В рубку должны назначаться древостой, достигшие возраста спелости леса. Такие древостой направляться вырубать вероятно стремительнее, не накапливая их в хозяйстве. Вместе с этим на период, не меньший числа лет в обороте рубки, должна быть обеспечена возможность неснижаемого количества лесопользования, включая все его виды.
в течении всего оборота рубки нужно иметь такое количество спелого леса, при котором возможно было бы при отводе лесосек выполнить лесоводственные требования (не превышать принятую ширину лесосек, сроки примыкания и т.д.).
Устанавливаемый размер лесопользования обязан по возможности снабжать полное удовлетворение потребностей народного хозяйства в древесине, заготавляемой в данном хозяйстве и тем самым содействовать большому применению действующих мощностей лесозаготовительных фирм.
Исходя из изложенных лесохозяйственных требований, опираясь на линейное программирование, В. Д. Волков и Д. Н. Дудин создали математическую модель, определяющую максимальное пользование лесом на ближайшие 10-летие и на целый оборот рубки. Математическая модель представлена ими совокупностью уравнений. Посредством их решается целевая функция (находится ее максимум) и дается последовательность уравнений, ограничивающих вероятный неистощительный размер лесопользования.
направляться подчернуть, что осуществление самого расчета по математической модели названных авторов вероятно только посредством электронно-вычислительных автомобилей.
Авторы модели советуют в качестве расчетной лесосеки размер лесопользования, отысканный указанным способом на ближайшее 10-летие. Результаты расчетов на более отдаленные десятилетия они вычисляют прогнозными размерами, подлежащими уточнению через каждые 10 лет.
Рассмотрение данных исследований В. Д. Волкова и Д. Н. Дудина разрешает заключить, что наровне с классическими способами, используемыми долгое время при установлении размеров годичного пользования лесом, за последние годы выявилось новое направление в ответе указанной задачи. Оно содержится в применении современного математического аппарата при учете многообразных лесохозяйственных факторов, воздействующих на размер пользования лесом, и исполнение громоздких и сложных математических действий посредством ЭВМ.
Расчетная лесосека определяется на целое 10-летие, именуемое в лесоустройстве ревизионным периодом. Благодаря этого вырубка древостоев, образующих расчетную лесосеку будет вестись несколько год, а целое десятилетие. В первоначальный год вырубят только 1/10 от количества рубок, запроектированных на 10 лет. Во второй и последующие годы рубка леса обязана вестись в таких Же размерах.
Последняя десятая часть запроектированного количества рубок будет вырублена на 10-й год по окончании лесоустройства.
Приведенные расчеты говорят о том, что не учитывая величины прироста спелых древостоев, оставляемых на корню на дополнительное пятилетие, размер расчетной лесосеки пара преуменьшается. В этом случае лес рассматривается в статическом положении подобно запасам угля нефти, других богатств и руды природы.
Определение расчетных лесосек по приведенным формулам ликвидирует указанный недочёт расчета.
Во снова осваиваемых районах таежной территории часто преобладают спелые и перестойные древостой. Их средний возраст возможно родным к естественной спелости. Такие древостой прироста не дают либо он образовывает малого величину.
В этих обстоятельствах поправка на пятилетний прирост в расчетную лесосеку не должна вноситься.