Николай чаварга о математических ошибках специальной теории относительности

В своё время Особая теория относительности была безо всяких неприятностей размещена в одном из самых солидных научных изданий современности, не обращая внимания на то, что постулат постоянства скорости света быстро противоречил и противоречит философии здравого смысла.

С течением времени возможности опубликовать статьи, основанные на философии нового мышления растут, а вот работы, основанные на здравом смысле — напротив, уменьшаются.

В наши дни сделать это уже фактически нереально, потому что на данный момент печатают по принципу: «Все мы согласны, что ваша работа безумна, но вопрос пребывает в том, достаточно ли она безумна, дабы быть у нас напечатанной».

Одна из немногих возможностей отечественного времени — это электронный издание «Мембрана». Имеется, но, подозрение, что те физики, от которых сейчас зависит будущее физических теорий, аналогичных изданий не просматривают, исходя из этого эта работа адресуется по большей части молодым физикам, для которых ещё имеется шанс освободиться от обморока нового мышления.

Главная задача теории относительности — обеспечить возможность описания некоего физического процесса либо события в понятиях, терминах, размерах, измеренных в движущейся совокупности координат, в случае если это событие либо процесс обрисованы в величинах и понятиях, измеренных в совокупности, считающейся неподвижной. К главным таким понятиям относятся время и пространство.

В случае если цена деления на шкале пространственной координаты и темп хода хронометра полагают не зависящими от состояния перемещения, то для сопоставления координат пространства и времени применяют совокупность уравнений (1), именуемую преобразованиями Галилея:

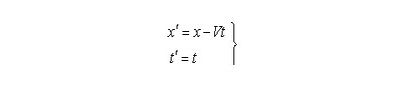
Совокупность уравнений (1). Преобразования Галилея.

Штрихованными знаками обозначены величины, измеренные в движущейся совокупности, в большинстве случаев обозначаемой знаком К?. Знаком К обозначают неподвижную совокупность координат.

Что касается физического смысла входящих в совокупность (1) размеров, тохимеет суть координаты произвольным образом выбранной точкиА(количество делений на отрезке от некоей точкиОдо точкиА), аt — это величина произвольным образом выбранного момента времени (количество тиканий хронометра от определённым образом выбранного момента, в то время, когда показания хронометра принимаются равными нулю).

Во всех теориях относительности принимают, что отсчёт времени начинается от момента, в то время, когда начала движущейся и неподвижной совокупностей совпадают:

Рисунок 1. Отсчёт времени начинается от момента, в то время, когда начала движущейся и неподвижной совокупностей совпадают.

Как мы знаем, преобразования Лорентца имеют вид:

Формула (2). Преобразования Лорентца.

Объединение уравнений в совокупность свидетельствует, что все входящие в формулы и одинаково обозначенные размеры имеют одинаковый физический суть.

В нашем случае это указывает, чтохв обоих уравнениях имеет суть координаты произвольным образом выбранной точкиА, аtимеет суть произвольным образом выбранного момента времени, причем между x и t нет никакой причинной связи. Обе размеры выбираются произвольно, но в каждом случае имеется собственная произвольность.

Как мы знаем, что механика Ньютона и теория Галилея прекрасно действующий при довольно маленьких скоростях перемещения.

Это указывает, что физический суть размеров, входящих в преобразования Лорентца, должен быть таким же, как и в преобразованиях Галилея, а при малых скоростях перемещения преобразования Лорентца должны переходить в преобразования Галилея.

Из первого уравнения совокупности (2) видно, что, в случае если пренебречь величиной V 2/C 2, то оно сходу переходит в пространственные преобразования Галилея.

Коэффициент негалилеевости (смотрите рисунок) определяет цену деления на шкале х?. На рисунке цена деления движущейся оси изображена вдвое меньшей, чем у неподвижной, исходя из этого вместоx? = x — Vt направляться писать x? = 2(x-Vt).

На первый взгляд думается, что подобные рассуждения возможно совершить и довольно второго уравнения совокупности (2). В литературе возможно отыскать следующий анализ.

В случае если по условиям задачи возможно вычислять, чтоV2/C2 пытается к нулю, то иV/C2 пытается к нулю. Из этого делается вывод, что произведение(V/C2) x кроме этого пытается к нулю.

Разумеется, что в случае если это верно, то второе уравнение принимает видt? = t, другими словами временные преобразования Лорентца при малых скоростях кроме этого переходят в преобразования Галилея.

В действительности данный анализ есть элементарно ошибочным. ЕслиV/C2 пытается к нулю, но не равняется нулю, то произведение(V/C2)x зависит ещё и от значения х.

Мы постоянно можем спросить таковой точкой, координата которой компенсирует малость величиныV/C2.

Опыт дискуссий говорит о том, что эта аргументация почему-то воспринимается не хорошо, исходя из этого проиллюстрируем сообщённое числовым примером.

Пускай мимо наблюдателя в неподвижной совокупности движется самолет со скоростью 900 м/с. По договоренности между наблюдателями хронометры запускают в тот момент, в то время, когда начала координат совпадают. Пускай мы интересуемся некоей точкой А, рисунок 1, на расстоянии х = 1016 м (это настоящая величина — расстояние до квазаров приблизительно на 10 порядков больше, ~ 10 26м).

Как преобразования Галилея, так и преобразования Лорентца, по идее, должны дать нам возможность найти значение координаты данной точки в движущейся совокупности в любую секунду времени, и показания движущегося хронометра, в случае если известны показания неподвижного хронометра, координата движения и скорость системы выбранной точки.

Для определения координатых?в моментt(к примеру, в моментt = 100 секунд) необходимо воспользоваться первым уравнением совокупности (1) либо (2) — в зависимости от того, в какой теории решается задача — в теории Галилея либо в теории Эйнштейна.

Разумеется, что итог вычислений в теории Эйнштейна будет пара громадным в связи с тем, что коэффициент негалилеевости при любых скоростях (не считая нулевой) больше единицы.

У нас нет сейчас претензий, исходя из этого не будем приводить вычислений пространственной координаты, отметим лишь, что расхождения будут очень малыми — в десятом символе по окончании запятой.

В случае если же мы желаем определить, какими будут показания движущегося хронометра через 100 секунд, то должны воспользоваться вторыми уравнениями совокупностей (1) либо (2).

В соответствии с теорией Галилея результаты измерений времени в обеих совокупностях совпадают всецело, t=t? = 100 cек.

В соответствии с теорией Эйнштейна вместо х необходимо подставить значение координаты произвольным образом выбранной точки, исходя из этого итог будет следующим:

Формула (3).

Полученный итог свидетельствует, что при скорости самолета 900 м/с (скорость современного самолёта) движущийся хронометр за 100 секунд не успевает сделать ни одного «тиканья»! Достаточно в уравнение (3) вместо х подставить 2*1016 м , как хронометр должен продемонстрировать минус 100 сек., для чего он обязан вращаться в обратную сторону, и без того потом.

Из всего этого возможно сделать лишь один вывод: потому, что преобразования Лорентца в виде совокупности (2) не переходят при малых скоростях в преобразования Галилея, они не являются корректными, исходя из этого не смогут использоваться для построения корректной теории.

Совокупность (2) – это главная математическая некорректность, на которой базируется теория относительности Эйнштейна. Все остальные математические неточности связаны с применением совокупности (2) для ответа разных задач теории относительности.

Первый вопрос, что появляется по окончании ознакомления с результатом, в большинстве случаев следующий: из-за чего подобная неточность оставалась незамеченной в течении практически много лет?

Одна из обстоятельств пребывает в том, что при ответе задач теории относительности задания по определению пространственной момента и координаты времени решаются раздельно — как не связанные между собой.

Наряду с этим в первой задаче величине х приписывают суть координаты произвольным образом выбранной точки (в действительности значение координаты задаётся условиями задачи, наряду с этим хне зависит от t), но во второй задаче данной же величине приписывают суть координаты, до которой перемещается начало движущейся совокупности (другими словами x = Vt ).

Иначе, при, в то время, когда делают диагностику того либо иного уравнения на инвариантность либо в то время, когда ищут выражение для сложения скоростей (среди них и для скорости света), в обоих уравнениях совокупности (2) под величиной х знают одну и ту же величину — координату произвольным образом выбранной точки.

Вторая обстоятельство пребывает в том, что величинахво втором уравнении совокупности (2) вправду должна иметь суть координаты, до которой за времяt перемещается начало движущейся совокупности, другими словами и в действительности x= Vt.

Это указывает, что задача определения показаний движущегося хронометра в большинстве случаев решается верно, исходя из этого неточность и оставалась незамеченной долгое время. В этом случае уравнение упрощается и принимает вид:

Уравнение (4).

Эта же формула получается и , если высказать предположение, что все элементарные частицы являются солитонные образования электромагнитного поля.

Электромагнитное поле, со своей стороны, возможно представить как «деформации», «натяжения» эфира. С этим предположением возможно выстроить несложную и непротиворечивую теорию относительности. Подробнее смотрите http://www.chavarga.iatp.org.ua.

Пара слов об экспериментальной проверке СТО. Формула (4) прекрасно подтверждается в опытах с быстродвижущимися мюонами, в случае если высказать предположение, что мюонам природой отведено за их время судьбы «определённое число тиканий», независимо от состояния перемещения.

В этом случае темп протекания всех физических процессов, среди них и темп хода

«мюонных часов», замедляется, и он успевает пролететь расстояние значительно большее, чем пролетел бы в соответствии с его временем судьбы в покоящемся состоянии.

При реально замечаемых в земных условиях скоростях мюонов, за время судьбы одного движущегося мюона в неподвижной совокупности успевают появиться и умереть приблизительно 10 покоящихся мюонов.

В соответствии с принципом относительности эффект должен быть лишь кажущимся, и движущемуся мюону должно было казаться, что за гибели мюонов и время 10 рождения в его совокупности обязан появиться и умереть лишь один неподвижный (которого он в праве вычислять движущимся).

В действительности опыт светло показывает, что «за одного движущегося 10 неподвижных дают», и представить обстановку в обратном порядке никак не удастся.

Так, опыты с мюонами очевидно противоречат выводам СТО, в соответствии с которой картина должна быть симметричной. Вместо экспериментального подтверждения мы имеем однозначное экспериментальное опровержение СТО.

Вторым экспериментальным подтверждением СТО вычисляют связь массы между скорости и тела перемещения. Эту зависимость легко взять в теории солитонов. Для этого достаточно высказать предположение, что масса частицы – это мера сконцентрированной в ней энергии.

Формула (5).

Обращаем, но, внимание читателя на то, что в данной формуле все величины измерены в одной (неподвижной) совокупности координат – штрихованные размеры отсутствуют. Это значит, что формула (5) не может служить инструментом для проверки теории относительности.

Она, по сути дела, просто не имеет отношения к теории относительности, как, к примеру, уравнение перемещения ракеты, которое обрисовывает перемещение тела с переменной массой.

В последнем случае масса тела все время значительно уменьшается, и в действительности этого мы не сомневаемся. Но с физической точки зрения это не принципиально. Уравнение Циолковского никто и ни при каких обстоятельствах не считал имеющим отношение к теории относительности.

Особая Теория Относительности

Темы которые будут Вам интересны:

• Множество теорий относительности, как 4х мерное подмножество моделей вселенной.

• Ошибки монтажа систем канализации и водоснабжения в частном доме

• Субъективное мнение опричинах отказа российской техники специального назначения. часть вторая

• Николай афанасьев: «необходима централизованная помощь в решении проблем застройщиков»