Сингулярность эддингтона, часть ii
( Часть I )
Да, … сингулярность Эддингтона,это как пограничный столб, где все что за ним — уже вне юрисдикции физической действительности. А перед ним?
Рис. 1. В отличие от математика, физик, в то время, когда что-либо находит, пытается пробраться в физический суть находки. «Физический суть» поясницы для сингулярности Эддингтона — это направление считывания кода. А узкая структура — носитель кода.
Довольно данной, физической стороны, исторически сложилось так, что первый физический суть электродинамической постоянной, представлялся конструктивным.
Т.е. так, как если бы практически целый заряд частицы, принимаемый за 1, был бы сосредоточен на ее периферии, за исключением dE = 1/n; где n – количество долей заряда. Так, заряд частицы (электрона) составлял «1», а содаваемое им магнитное поле, было меньше расчетного на 1/n. Что и было найдено в опыте по узкой структуре уровней энергии водородоподобной модели.
Исходя из этого, отысканная безразмерная константа и была названа: постоянной узкой структуры.
Это что касается замечаемых физически особенностей сингулярности — как материальной точки. Наряду с этим, хотелось бы отметить исключительноось самой постоянной узкой структуры в физике. Так, к примеру, она связывает между собой три фундаментальные размеры:
Но, к делу.Потому, что задача отыскать физический суть данной величины, перед нами не следует, всевозможные мнения, довольно физического смысла данной величины, пока покинем.
Мы сейчас вне области физики и более того, вне математического формализма – языка физики. Принято вычислять, что предметами для того чтобы рода занимается философия, в частности – метафизика. Но и с этим нельзя согласиться.
Метафизика, дословно: «то, что перед физикой», т.е., как бы, прикладная философия – раскрывает самые неспециализированные правила физической картины мира, типа — из-за чего и для чегои кому это необходимо?
Говоря сухим административным языком, это вопросы, интересующие потребителей и законодателей. А нас интересует вопросы как бы второго сорта: ремесленные, вопросы исполнителей – как и что делать, что б придуманные вами законы неукоснительно исполнялись?
Так как как раз этим, по большей части, занята психика организма – она не формирует законы, а реализует адекватный ответ на внешние, строго «законное» действие. Так как противодействие организма лишь тогда будет адекватным, в то время, когда не выходит за рамки «закона» и руководствуется «законом».
Так, отечественный предмет – этоисполнительная составляющая объективной действительности. Т.е. все то, что в соответствие с принципом основания (лезвие Оккама), считается избыточным. Вправду, для чего физике знать аккуратный контент, в случае если открываемые ей законы, просто не могут нарушаться.
Само собой разумеется, физикам легко – их не интересуют явления психики, но отечественная сложная – продемонстрировать, что специфика психологических явлений, это не функция материи, а сама материя. Что психика – это такой же феномен действительности, что и феномен жёсткого тела. По крайней мере, феномен жёсткого тела и феномен сознания — явления одной природы.
___________________
И без того, сингулярность Эддигтона – это вакансия (безлюдная точка) в 3-х мерном Евклидовом пространстве, задающая координаты материальной точке, конечно, узкая структура материальной точки – физический носитель личного кода, по которому точка может занять собственную вакансию.
Выяснив так сингулярность Эддингтона возможно перейти к оценке мощности множества «тяжелых» частиц во Вселенной, как их именовал Эллингтон.
Рис. 1. Сингулярность Эддингтона – информационный нюанс.
Ну вот, мы «пересекли» область физики, «пересекли» Евклидовом пространстве, и появились в информационном «пространстве», области теории совокупностей и кибернетики.
На рис. 2 представлена узкая структура физической точки, способная нести неповторимый код частицы. Тут любой материальный фрагмент частицы соответствует одному бинарному (самый несложный алфавит) знаку 0/1.
Начало кода обозначено вакансией, что образуется при помещении одной из частиц носителя кода в центр окружности. В данной схеме физический спин материальной точки возможно трактовать, как направление считывания кода (продемонстрирован стрелкой на рис. 1).
Рис. 2. Так как прямая линия в топологии отечественного множества не выяснена, мы можем пользоваться лишь окружностями.
Что бы взять расстояние R – радиус равноудаленного множества точек {L}, мы должны воспользоваться запасным окружностью диаметра R, так что фактический радиус равноудаленного множества точек оказывается равным 3.14хR
Увидим, что в информационном пространстве любой элемент – это некое подмножество. Так как все что тут существует, в соответствие отечественной исходной и единственной теоремы, в МВМ не существуе ничего не считая подмножеств. Исходя из этого, в информационном «пространстве» любой элемент узкой структуры – это собственный подмножество точек.
В каждом таком подмножестве мощность личных кодов каждого элемента однообразны, (в действительности, точки верно было бы разглядывать как фрактал, но не будем пудрить мозги: сущность дела от этого не изменяется). Исходя из этого их возможно изображать, как окружности – в соотвтствие с определением: окружность – это множество точек, равноудаленных от одной из них, лежащей в центре.
Соответственно, в случае если нужно отложить радиус взятой окружности, то и он также должен быть образован такими же подмножествами (на рис.4 изображена «топ-модель» отечественной сингулярности в информационном «пространстве»).
Рис. 3. Между информатикой и физикой. Топология подмножеств, образующих сингулярность Эддингтона, в информационномпространстве стала называться – «клейн».
В честь династии математиков, чье имя стало популярным как раз благодаря сосуду Клейна.
Так как и разглядываема фигура конкретно связана с топологией сосуда Клейна – как геометрического образа топологии МВМ.
Фактически, все нужное для определения мощности множества всех тяжелых частиц Вселенной, нами оговорено. Приступим к ответу.
Т.е. определим длину личного кода частицы при которой ее геометрический образ вправду есть окружностью: т.е. множеством равноудаленных точек.
Ответ
к определению n методом последовательных приближений.
Радиус окружности множества равноудаленных точек мощностью {n} возможно выяснить как количество информации (в битах), нужное и достаточное для однозначной индексации каждой точки, образующих окружность:
R = log2(n)[1].
Соответственно,протяженность окружности L = 2 x П x R [2]
(Где П – число «Пи», что б не было путаницы при копировании в формат блокнота ).
Потому, что, любой структурный элемент окружности образован своим подмножеством, выстроенном на отрезке дуги, как на диаметре, количество этих элементов будет в Пи раза больше, чем если бы они были выстроены из точек громадной окружности L, взятой из [2].
Так, формула для расчета количества элементов окружности примет вид:
n =L x П = (2 x П x R) x П = 2П^2 xR [3]
Подставив значение R из [1], возьмём уравнение для n
n = 2П^2xlog2(n); [4]
Вот и все. Чтобы не париться с преобразованиями, решаем способом подбора (последовательных приближений – итераций, по-научному).
Ну, это вы сделаете сами – в помощь, вот эта страница из презентации в финале общероссийского конкурса «Юниор» (МИФИ 2007год, думается).
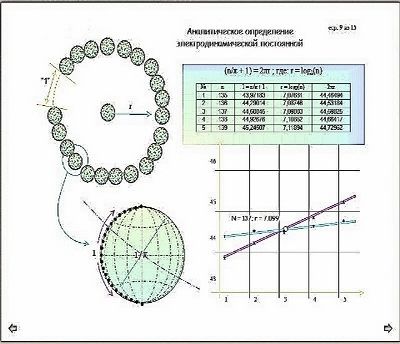
Рис. 4. Слайд из презентации «квазифизическая природа сингулярности», приблизительно 2003 — 2007 гг.
В следствии, вы придете к проблеме, которую хотелось бы пояснить. Дело в том, что число Эддингтона, рекомендованное им самим, равняется приблизительно 10^80, а у вас оказаться:
Na = 2^137, что приблизительно равняется: 10^40, т.е. на 40 порядков меньше — не слабо!
Это не неточность, а новая информация к размышлению:общее число тяжелых частиц во Вселенной, это не количество наблюдателей (10^40), а количество их взаимонаблюдений – по Дж. Харликару. Т.е. Na^2 = (10^40)^2 = 10^80;
Что требовалось продемонстрировать.
(Продолжим по окончании перерыва)
_____________________________
Так что сейчас упреки в мой адрес, что я что-то недоговариваю, не принимаются.
Ну и как мы уже условились, пока на этом: благодарю за внимание.
Рис. 5. Для программиста данный объект именовался легко «куб», либо 3-х мерное отображение 2-х мерной энграммы. Это и имеется «куб Клейна» — символическое изображение главного элемента программы «хаос-архиватор».
Тут методом совокупности транспозиций, на субквантовое мгновение, время и пространство, как бы,изменяются местами.
Продолжение, правильнее выводы и заключение – в третьей части работы, посвященной сингулярности Эддингтона. В том месте мы подробнее определим про «куб» и «сингулярность Клейна».
Ну и думаю, самое захватывающее — наконец-то возможно будет неформально разглядеть программу «хаос-архиватора».
Ну и последнее: вот данный натюрморт, что так поразил воображение сотрудника, что: «рад был бы совершить ошибку» (из части I).
К сожалению,источник узображения утерян.
Вправду, имеется маленькая хрустальная (без ковычек) сфера, линейно расширяющийся сосуд и фужер Клейна — отечественный знак МВМ (действительно, стекдув мало перестарался со стилизацией в пользу практичности).
ПОСЛЕСЛОВИЕ — 3 дня спустя.
Статья вышла, по причине того, что не имела возможности не выйти – в противном случае неформального введения в хаос-архиватор не окажется. Сперва, считал, что смогу обойтись 2-3 одним рисунком и страницами текста – тот что с «колесами» как у велосипеда, после этого оказалось 3 части. Сейчас вижу, что просматривать это нереально.
Само собой разумеется: путь от сосуда Клейна к стилизованному сосуду, где линия пересечения поверхности стянуто до одной безлюдной точки – точки проникновения, занял у меня пара лет. А сейчас все это нужно выразить на одной странице. Само собой разумеется не получается.
Но иначе, это имеется необходимость: сингулярность Эддингтона, потому и сунгулярность, что в ней не одна точка, а сходу три, поделённые лишь временем. Так как что такое сосуд Клейна – это глобус, у которого южный полюс вдавлен до касания изнутри где-то на меридиане, а северный – вытянут до касания с той же точкой на меридиане, где изнутри к ней подходит южный полюс. (рисунка не будет – и без того через чур всего большое количество, имеется презентации). Между этими полюсами, в том месте где они смыкаются на меридиане, образуется безлюдная точка, находящеяся в собствености несложной поверхности данной сферы.
По-видимому, эта безлюдная точка и имеется сингулярность Эддингтона, которая разворачивается во всю поверхность сосуда, т.е. во все Множество. Для сферической поверхности имеется образующая – вот именно она и проходит через сингулярность, заканчиваясь и начинаясь в соприкасающихся полюсах.
Но, поскольку это не просто точка проникновения, а точка проникновения через одностороннюю поверхность. Если бы тут было бы горлышко сосуда – то мы имели возможность вырезать лист Мебиуса, но у нас лишь одна безлюдная точка, так что лента не окажется – у линии нет сторон! Исходя из этого мы сходу приобретаем удвоенную длину (в случае если лист Мебиуса разрезать на протяжении, то окажется не два сплетенных кольца, а одно, закрученное и удвоенной длины).
Помимо этого, эта образующая «закручена» – как бы имеет «спин».
Т.е. я желаю заявить, что в физической интерпретации этого явления имеется некие совпадения с теорией суперструн.Но нам это как бы до лампочки. Нас интересует второе – что исследуют физики, в то время, когда «накачивают» энергией фундаментальную структуру материи? – это во-первых, и во-вторых: как выйти на динамику и топологию МВМ?
С первым, достаточно легко: тут физики проходят в «отечественную область» – т.е. область физически несуществующих объектов, образов МВМ, каковые хоть как-то смогут быть идентифицированы с формами существования материи.
Конечно, без математики, никакие эти образы не существовали бы. Но они и не существуют – время судьбы их очень ограничено.
Исходя из этого и нет никакого бозона Хигса – нет и не может быть физической интерпретации того, что придает саму материальность фундаментальной структуре. Разве что как в сказке Льюиса Кэрролла, где существовали два взаимоопределяющиеся братца.
А вот со вторым – сложнее. Несложнее до тех пор пока принять на веру, что координата точки проникновения записывается в виде бинарного кода, формируемого «наблюдателем». Коим есть окрестность данной точки, разглядываемая статистически .
Хорошо, я осознаю, что все это похоже на абсурд. Ну, что ж. Основное, как сказал Нильс Бор: «не имеет значения – веришь ты в это, либо нет, основное что трудится». А суть возможно и придумать.
По крайней мере, в последней III-ей части буде продемонстрировано, как это трудится.
Ну а в целом, будем вычислять, что и вторая попытка неформального введения в мировоззрение, где объективная действительность представлена двумя дополняющими качествами: «мнимым» и «настоящим» — провалилась.
Что ж, будем пробовать опять и опять. Потому, как без таких представлений, сознание ни при каких обстоятельствах не будет рассматриваться, как что-то, талантливое к переходу на другой носитель, а без для того чтобы рассмотрения, нельзя сформулировать требования к технологии перехода и аппаратному обеспечению, где ведущую роль играется психология. А следовательно, и нет предмета изучения.