Недокументированные возможности цифрового кодирования аналоговых сигналов.
Плата Искра 015-14 (АЦП) в открытом виде от МикроЭВМ Искра 226.
«Недокументированные» возможности цифрового
кодирования аналоговых сигналов.
Финиш ХХ века стал началом так называемой «цифровой эры» и на данный момент от цифрового кодирования аналоговых сигналов уже некуда не убежать. Не смотря на то, что у меня до сих пор дома стоит простой магнитофон, я уже в него лет пять не вставлял кассету и использую его в качестве колонок компьютера.
И не смотря на то, что изображение на экране дисплея с каждой заменой видеоплаты делается все лучше, а звук все чище — при каждой замене звуковой платы (увы, встроенным кодеком материнской платы не пользуюсь), не смотря на то, что способ аналого-цифрового и цифро-аналогового преобразования не изменялся с самого момента его изобретения, хотелось бы к известным знаниям добавить собственные мысли по увеличению его качества и точности. Это не означает, что я ставлю под сомнения теорему Котельникова, где говориться, что частота дискретизации для правильного аналого-цифрового либо цифро-аналогового преобразования должна быть как минимум в четыре раза выше нужной верхней границыполосы пропускания, просто так оказалось.
Как Вы понимаете, при простом цифровом преобразовании аналогового сигнала, данный сигнал представляется легко фиксированными размерами применяемого физического
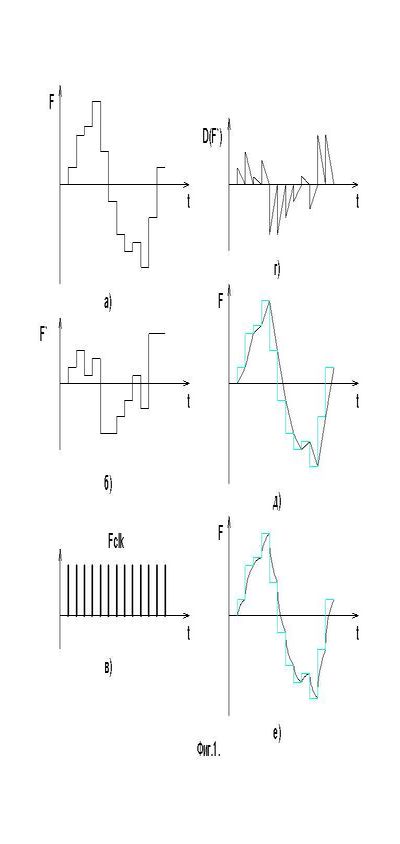
Рисунок 1. Осциллограммы аналогового сигнала с выхода ЦАП до и по окончании применения способа с аппроксимацией, конечно сопутствующие дополнительные сигналы.
Рисунок 1. Осциллограммы аналогового сигнала с выхода ЦАП до и по окончании применения способа с аппроксимацией, конечно сопутствующие дополнительные сигналы.
параметра F, к примеру электрического напряжения, однообразной длительности, т.е. с каким-то периодом, что на данный момент принято характеризовать наименованием «частота дискретизации» (Fclk на фиг.1в). Как видим из рисунка фиг. 1а, получается череда угловатых столбиков, каковые хотелось бы сгладить, и я взял на себя смелость предложить кодировать вместе с главной величиной оцифрованного сигнала дополнительно еще и его производную F` (фиг.
1б), что разрешит аппроксимировать сигнал (фиг. 1д). Само собой разумеется, для записи данной величины в обязательном порядке понадобитсядополнительное поле разрядности m к полю главной величины разрядности n в памяти либо файле. Разрядность m предполагаю маленькую, но в первых микрокомпьютерах также вычисляли верхом мечтаний 16 цветов на точку либо пиксел.
Кстати диапазон величины производной либо наклона вершины столбика будет варьироваться нечетным числом дискретных уровней, поскольку три дискретных уровня, соответствующих наклону 90°, 0°, -90° необходимы. Это очень некомфортно на мой взор для бинарной совокупности счисления, поскольку в обязательном порядке «меньшая добрая половина» вероятных значений отведенных полей памяти разрядности m будет избыточна и не использована. Со своей стороны модуль тангенса для пределов 90°, -90° будет равен бесконечности, исходя из этого их определенно никто не будет применять, соответственно мои опасения, само собой разумеется, напрасны.Но не будем мешать делать программистам собственную работу и разглядим аппаратную часть для реализации цифро-аналогового и обратного преобразования.
Аппаратная часть для цифро-аналоговогопреобразования представлена на фиг.2.
Рисунок 2. Схема ЦАП с добавлением составляющей производной сигнала.
Рисунок 2. Схема ЦАП с добавлением составляющей производной сигнала.
Тут мы видим общепринятые входные регистры-защелки RG, блоки стандартных ЦАП DAC и выходной фильтр частоты дискретизации, каковые для каждого ЦАП необходимы,
разве что удваивается количество первых двух блоков RG, поскольку добавлено новое поле. Цифровые информацию о производной сигнала DATAS преобразуются простым методомв аналоговый сигнал и через ключ SW поступают на управляемый уровнем генератор треугольных импульсов G, что из-за указанного выше ключа возможно назвать стробируемым. В следствии приобретаем сигнал D(F`), изображенный на фиг.
1г, что нужно проинвертировать и суммировать с главным знаком величины (поле DATA), для чего мы эти сигналы на инверсный и хороший вход операционного усилителя, что сходу делает функции сумматора и инвертора либо вычитателя, и усилителя. С выхода данного усилителя мы приобретаем в принципе уже готовый сигнал, что требуется очистить от частоты дискретизации Fclk фильтром F1.
Аппаратная часть для аналого-цифрового преобразования на фиг. 3 сама просится на язык и не должнапредставлять для реализации полностью никакой сложности, поскольку
схема направляться из сути способа. Сигнал поступает на один обычный АЦП конкретно и через дифференцирующую схему D — на другой. В следствии приобретаем обе составляющие главной величины DATA и производной DATAS, каковые выбираются из АЦП и помещаются в память любым известным способом.
Хотелось бы подметить, что блок генератора треугольных импульсов G и блок дифференцирующей схемы D в схемах на фиг. 2, 3смогут быть выполнены, как
Рисунок 3. Схема АЦП, учитывающего величину производной сигнала.
Рисунок 4. Несложный дифференцирующий блок в виде RC-цепи.
Рисунок 3. Схема АЦП, учитывающего величину производной сигнала.
Рисунок 4. Несложный дифференцирующий блок в цепи и-виде.
тривиальные дифференцирующие RC-цепи (фиг. 4). При применении данного варианта
вероятно нужно включение перед их входом буферных усилителей подобных буферному повторителю BF для повышения надежности. Кроме того, RC-цепь не есть совершенным формирователем треугольных импульсов, исходя из этого аппроксимация будет происходить не прямыми отрезками, а кусочками экспонент, как нарисовано на фиг. 1е.
Рисунок 5. Осциллограмма сигнала с несогласованной производной.
Рисунок 6. Схема блока сглаживания сигнала с выхода простого ЦАП.
Рисунок 5. Осциллограмма сигнала с несогласованной производной.
Рисунок 6. Схема блока сглаживания сигнала с выхода простого ЦАП.
При применении обрисованного способа рассчитывать производные, к примеру, для изображения компьютера будет достаточно трудоемко, соответственно, само собой разумеется найдется мало желающих трудиться с изображением с применением всех предлагаемых возможностей, но это возможно нормально взвалить на плечи графического ускорителя, для современных систем он стал нормой. Ну и само собой разумеется, точно покажутся хитроумные методы обработки изображения, но, снова повторюсь, не будем забегать вперед и отбирать работу у программистов, программисты – также люди.
Помимо этого, в следствии избыточности кодирования сигнала, к примеру изображения компьютера, возможно приобретать всевозможные эффекты, изображенные на графике фиг. 5, каковые, быть может, не всегда будут желательны. Соответственно появляется предположение: «а не хватило ли бы нам легко схемы, изображенной на фиг.
6?». Тут сигнал со стандартного ЦАП (вход IN) подается сходу на хороший вход операционный усилителя SM и через дифференцирующую схему D – на отрицательный. В следствии на выходе усилителя возьмём сглаженный сигнал, что дополнительно будет отшлифован фильтром F1.
Но в обязательном порядке найдутся знатоки, каковые обзовут данную схему «суррогатом», исходя из этого считаю, что в устройствах класса «PRO» должны быть реализованы оба способа, разве что последний блок с фиг. 6 нужно сделать отключаемым, к примеру с помощь разряда какого-нибудь порта вывода управляющего процессора либо однобитового поля видеопамяти. Результирующая схема изображена на фиг.
7 и отличается от схемы на фиг. 2 наличием аналогового мультиплексора сигналов с
Рисунок 7. Итоговая схема многорежимного ЦАП с способом аппроксимации.
Рисунок 7. Итоговая схема многорежимного ЦАП с способом аппроксимации.
выходов схем G и D, каковые подключены к выходам ЦАП главной величины и ЦАП производной. Эти схемы смогут быть выполнены одинаково, как на фиг. 4, ноих параметры для верной работы устройства требуются различные. Одна из них трудится, как генератор треугольных импульсов с фиг.
2, а вторая, как дифференцирующая схема с фиг. 6. Соответственно их совместить не окажется и было нужно установить сходу обе. Выход данного аналогового мультиплексора, собранного на ключах SW и управляемого битом режима DATAM дополнительного входного регистра, фиксируемого по фронту сигнала Fclk, подключается к отрицательному входу выходного операционного усилителя SM, как в схеме на фиг.
2. Отключать ЦАП производной возможно легко подачей нулевого значения DATAS и особых схем для этого не нужно.
И вот, надеюсь, не так долго осталось ждать настанет время наслаждаться отличным изображением на экране монитора. Эти способы в обязательном порядке разрешат избавиться от пресловутых пикселов компьютерного изображения. Если бы эти способы были бы применены при формировании изображения сходу на самых первых моделях ЭВМ, быть может, их программами пользовались бы до сих пор, не морщась по окончании изображений с современным качеством.
Плавные переходы между пикселами сделали бы собственный дело.Само собой разумеется, остались буквы, без которых не обойтись и каковые должны отображаться с прошлой резкостью переходов, но кроме того тут программисты реализуют методы сглаживания, каковые возможно частично переложить на плечи выше обрисованных схем. Я думаю, не следует напоминать читателю о TV-тюнерах, FM-радио платах, звуковых кодеках, сканерах и без того потом, везде при применении вышеописанных «недокументированных» возможностей цифрового кодирования аналоговых сигналовнас ожидают завораживающие и радужные возможности.
Ссылка: http://technic.itizdat.ru/docs/mer/FIL12911798460N843349001/1
либо сходу *.pdf.







