Oбразование современных форм геномов оптимизация
ЭВОЛЮЦИЯ
Oбразование современных форм геномов — Оптимизация
ВВЕДЕНИЕ
В данной работе совершён анализ направленности преобразований в геномах . С целью этого создана модель-принцип оптимального кодирования . Изучено наличие соответствия между математической моделью и настоящими геномами .В следствии сделано заключение о соответствии модели спектрам распределения A,T и C,G мультиплетов в настоящих геномах .
Неспециализированная ЧАСТЬ
ИНФОРМАЦИОННОЕ СОВЕРШЕНСТВО
в генетике
Продолжая неспециализированную идею IP ( Информационного Совершенства ) , создатель разглядывает вопросы кодирования в геноме .
светло 1 , что источником эволюционного материала и разнообразия ДНК было мультиплицирование разных по размеру кластеров 1, целых хромосом а также целых геномов 2,3. Кроме этого разумеется , что геном должен ‘защищаться’ от произвольного ‘применения’ в нём адресных векторов (AV) .
Оптимальное кодирование
Разглядим следующую проблему в развитии генома ( родственную проблеме в информационных разработках) – которую назовём ‘оптимизацией кода’ . Дабы обеспечить ?ровный? процесс развития через мутации ( каковые неизбежно последуют мультиплицирование в геноме ) , геном , принаращивании собственной долги , должен был оптимизировать длину ‘адресного слова’ . При через чур долгом адресном векторе , процесс их ?подгонки? ( ?присвоение нового адреса?) быстро замедляется , так как новый ?ген? мешает работе ветхого , а ветхий новому . Обратно , при через чур маленькой длине , через чур легко , в различных местах генома , в ходе мутации , появляются ?нелегальные? адресы : что быстро усложняет работу генома , его его эволюцию и адаптацию . По данной причине , геном должен ?решать? проблему оптимизации кодирования . Можем записать следующее уравнение для всех данных в геноме :
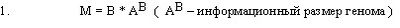
Где : M – физический размер генома ;
A — код ;
B — большой физический размер адресного слова (AV) .
Оптимум этого неспециализированного уравнения будем искать при условии : B*A = Const ( которое соответствует информационному размеруAV ). Тогда при условии :
2. B * A = Const
будет достигаться при:
Другими словами , при повышении размера генома , ‘А’ – пытается к‘е’ .
Тогда :
Первичная совокупность была по-видимому двойничной 2 , другими словами , сперва главный код был двойничным – А , Т(U) . Современная совокупность четверичная — A,T(U),C,G . Весьма интересно , дабы выйти из этого положения ( и сохранить принцип оптимальности), природа должна была каким-то образом , при двойничной совокупности: ‘расширить’ значение кода , а при четверичной: ‘уменьшить‘ его . Создатель предполагает , что один из самые приемлемых вариантов в двойничной совокупности было – применение модифицирования одного из нуклеотидов А ( до А*- вероятно С ? ) либо Т ( до U ) .
Совсем не обязательно дабы ‘новые‘ нуклеиновые основания (НО) были сходу ‘вписаны’ в копируемые комплементарные пары , а как на данный момент : метилированные основания в ДНК расширяют возможности ‘сжатия’ совокупности управления и , производятся лишь на время реализации процессинга . Таковой вариант предполагает наличие инструментария , азначит , по всей видимости , существует ‘другая’ модификация НОи пептидов , с участием лишь ионов металлов , несложной органики и РНК .
Из уравнения (3) возможно выяснить уравнивающий коэффициент , для размерности — `Z`:
Где : K – коэффициент размерности (для (2),К = 1,44 ; для (4) К = 0,72 )
и уравнение (4) запишется в виде :
Коэффициент ‘K’ – имеет суть – уравнивающего коэффициента к основанию ‘Z’ до оптимального основания — ‘е’.
Это значит , что в случае если мы исследуем график разложения одноморфных геномов в координатах : Bi– Ln ( M) , то углы наклона будут соответствовать степени приближения либо к двойничной (1/К = 0,693 ) , либо к четверичной ( 1/К= 1.4 )совокупности Фиг 1.
Запишем уравнение (6)в виде :
7. Ln ( Mb / Bi ) =K*(Bi-1)*Ln Z
Где : Mb – гипотетический геномный размер
Наряду с этим : K * (Bi-1)–подлинный (информационный либо математический) размер вектора AV . Отношение:Mb / Bi = n — число AV размером ‘Bi’ , ‘Mb’ –длянаснеобходимо для изучения подлинных геномов , каковые прошлидолгий , метаморфизирующийпутьэволюциии , исходя из этого , будут иметь динамическую картину , различающуюся от ?чисто? теоретической .
Динамическая картина включает в себя всю предисторию данного генома ( к примеру , в случае если этот геном имел в собственной истории дублирование нескольких хромосом либо целого генома , он должен был ?выработать ? последовательность долгих векторов, но при утрата громадной части генома в последующем развитии он, вполне возможно , сохранит их а также может ?нагрузить? их дополнительными функциями ) .
Тогда уравнение (7) будет выглядеть следующим образом:
8 Ln (n i) = AV * Ln без сомнений
где : n i – число векторов типа (i).
AV — информационная долга i-го вектораBi
При ?путешествии? во времени подлинный геном будет генерировать последовательности векторов , так как ветхие векторы заняты( кроме того как последовательности организации ) и возможно ожидать , что при образованииновых семейств генов будут образовываться и новые семейства векторов ( лишь их размеры , для удовлетворения условию оптимальности будут стремиться быть пропорциональными текущему размеру генома ( формула 4.)) . В координатах — Ln (n i) — AVi, угол наклона будетравен : tg= Ln Z . Всё это указывает , что замечаемый размер AV и генома (физический) не соответствует математическому , из-за ?проходящего? размера генома . Иначе , уравнение (7) – воображает второй вариант доказательства уравнений распада ?платформ? представленный в работе 1.
Иначе , изломы на графике Ln(n) – AV , показывают на ?разные? регионы в которых действуют эти векторы. Другими словами , разные подлиневекторы – трудятся и на различныхучастках , причемэти участки имеют очень сильно отличающиеся размеры .
К примеру , разглядим график 5А – Dros.Melan. .
Кроме этого , очевидно существует последовательность сопряженных векторов , тогда их размер уже являетсясуммой двух и более размеров подлинных размеров . Все эти явления в один момент наблюдаются в геноме и уточнение вектора развития адресной части информации уже является заведомо сложную задачу и испытывает недостаток в детальном изучении . Иначе , определение типа адресного вектора разрешает выяснить возможности развития генома . Углы наклона графика Ln(ni) – Bi , по окончании первого излома несут в себе и данные о скорости трансформации ( другими словами мутационную активность ) в тех кластерах где трудятся эти вектора .
Анализ геномов
A , T — мультиплеты
Из анализа графиков (Graf 1-8) и таблицы ,видно, что наклон (К) ?А? и ?Т? на начальных ветвях мультиплетов ( размер 1 до ~ 8 , до точки первого излома ) бактерии E.Coli находится в пределах : 1,22 — что есть родным к норме Z = 4( но меньше её ) . У Тularemia : К = 1,0 ( Что дает Z=е ). У Giardia lambliaв пределах : 1,38 — что еще ближе к Z=4. Fungy кроме этого имеют громадное разнообразие в ?К?: Candida (1.1), SACCHAROMYCES CEREVISIAE (1.01), Yarrowia lipolityca (1.26). Насекомые ,?К?~ 1 : Anopheles gambae (1.12),Apis mellifera (0,98), D.Melanogaster(1.03). Рыба- Фугу (1.2) .У более развитых форм геномов еукариотов ?К?весьма близко к~ 1 : Human (1.07),Mouse (1.1),Gallus gallus(1.06),Canis familiaris( 1,007) .
Синтез пептидов
В случае если разглядеть начальный период развития судьбы , то неприятность ?оптимизации? встретилась и на этапе появления протеинового синтеза . Повторяющиеся ?коды? протеиновых последовательностей вынудили RNA-DNA совокупность создать ?оптимизированный код? для действенной работы механизма синтеза белков. И , по всей видимости , все еще существует ?другой синтез белка ? ( RNA Driving Peptides ?RNA-DP? ) исполняемый лишь RNA(по всей видимости подобными ncRNA либо rRNA + ионами металлов ( по всей видимости : Ca , Mg ) и АТФ -АДФ- АМФ. Таковой синтез, возможно, трудился для главных ?древних? аминокислот, предположительно кодируемых лишь A и U(T) основаниями :
AAA — Lisine, AAU-Asparagine , AUA-Isoleucine , AUU- Start, UUU-Phenylalanine ,UUA- Leucine , UAU-Tyrosine , UAA-Stop; ( предположительно и UCU(A)-Serine,CCU(A)-Proline , CAU-Histidine ,CAA-Glutamine , ACU(A)- Threonine , ) .
Для случая промежуточного ?кодирования? пептидов , уравнение (4), в смысле оптимума при `е`, снова будет справедливо , лишь код будет складываться из трех нуклеидов четверичной совокупности ( A,U,C,G) .
где : Np – число кодируемъх функций , Bc = 3 .
Приобретаем:Np = 20,1 , по таблице кодонов имеем : 20 аминокислот + 6 дополнительных фукций , что намного ближе к истине чем простое : 43 = 64 .
Так , возможно с уверенностью утверждать , что одной из движущих сил эволюции генома есть удовлетворение критерию?оптимального? кодирования . Отличие мутационной подвижности в разных частях кластеров может быть около десяти порядков ! Это косвенно показывает на неспециализированную нестабильность геномов и их высокую пластичность.
Выводы
Эволюция геномов очевидно управляется неспециализированным довлеющим причиной – повышение компактности информации в геноме . Это достигается по большей части уравновешением соотношения A,T / C,G ( Что позволяет без проблем реализовать компактности и принцип оптимальности) . И оптимизацией размеров адресных векторов , каковые , так , становятся главным кодирующим размером генома . Сам механизм `мягкого` действия этого фактора и есть одним из инструментов эволюции .
Так , развитие преследует комплект многообразных целей . Часть из них связана с информационнымсовершенством генома :
1. Большое применение информационного размера генома .
2. Оптимизация размеров кодирования функций .
3. Оптимизация кластеров размеров ( и группы генов ).
Подтверждается неспециализированный вероятностный темперамент векторов развития генома .
REFERENCES :
1. Susumu Ohno «Evolution by gen dublication».
2. S. Astashkin « EVOLUTION , formation of modern forms GENOMEs»- Эволюция, образование современных форм геномов 2006г.
3. S. Astashkin «Эволюция эволюции».







