Парадокс конвертов губит природную симметрию случая
Двое исследователей из Австралии нашли перспективный подход к 80-летней тайной, объяснение которой может иметь последствия для массы теоретических и прикладных областей: от наглядного понимания некоторых оптимизации работы и парадоксов термодинамики технических совокупностей до улучшения электронных составления и схем победной стратегии игры на фондовом рынке.
Именуется эта тайная «Парадокс (неприятность) двух конвертов» (Two envelopes problem). В формулировках и различных вариациях она известна математикам с 1930 года, не смотря на то, что как раз в виде двух конвертов была обрисована лишь в конце 1980-х.
Итак, играем. Вам предлагаются два конверта с деньгами (взвешивать, ощупывать и просвечивать их, ясно, запрещено). Вы понимаете лишь, что в одном из них содержится сумма ровно в два раза громадная, чем во втором, но в каком и какие конкретно как раз суммы — совсем неизвестно.
Вам разрешено открыть любой конверт на выбор и посмотреть на деньги в нём. По окончании чего вы должны выбрать — забрать себе данный конверт либо обменять его на второй (уже не глядя).
Вопрос — как вам поступить, дабы победить (другими словами взять солидную сумму денег)? Думается, что шанс на проигрыш и выигрыш неизменно однообразен (50%) независимо от того, покинете ли вы себе открытый конверт либо заберёте вместо него второй.
Так как возможность нахождения большей суммы в конверте A изначально такая же, как возможность, что более внушительные деньги лежат в конверте B. И открытие одного из конвертов (A) ничего не может сказать вам о том — видите вы солиднейшую либо мельчайшую сумму из двух предложенных. Но вычисление средней ожидаемой «цене» второго конверта говорит об другом.
В совершенстве конверты должны быть однообразными, чтобы исключить отвлекающие от сути неприятности рассуждения игрока о том, в какой из двух конвертов ведущий захотел бы положить солидную сумму, а в какой – меньшую (фото с сайта Wikimedia Commons).
Допустим, вы заметили $10. Значит, в другом конверте лежат или $5, или $20 с возможностью 50 х 50. По теории возможности средневзвешенная сумма в конверте B равна: 0,5 х $5 + 0,5 х $20 = $12,5.
Очевидно, открыв другой конверт, вы заметите не эту сумму, а или 20, или 5 американских долларов, легко по условиям игры. Но 12,5 — такова (по вычислениям), как думается, будет средняя сумма выигрыша на кон при проведении большого числа раундов, если вы постоянно будете поменять конверты.
И результат не зависит от начальной суммы денег. Так как в различных раундах смогут употребляться различные пары (10 и 20, 120 и 60, 20 и 40, 120 и 240 и без того потом). Другими словами в общем виде, в случае если в конверте А лежит сумма С, то статистически ожидаемая сумма в конверте B составит 0,5 х С/2 + 0,5 х 2С = 5/4 С.
Так, теория говорит, неизменно выгодно поменять начальный собственный выбор (12,5 больше 10), не смотря на то, что в отдельных раундах вы станете проигрывать. Но против для того чтобы вывода восстаёт интуиция, которая о принципиальном равенстве конвертов. Так как поменяв их вы имеете возможность начать все рассуждения сперва (не открывая второй) и поменять опять.
На разрешение данного парадокса несколько раз претендовали разные учёные. Более того, идут кроме того споры о том, как осознавать — в чём тут содержится сам парадокс. Но математическое сообщество до сих пор не пришло к консенсусу, так что задача осталась открытой.
Сейчас же собственную разгадку (вернее, подход прикасаясь к её окончательному разрешению) и собственное видение подводных камней данной неприятности внесли предложение Марк Макдоннел (Mark McDonnell) из университета Южной Австралии (University of South Australia) и Дерек Эбботт (Derek Abbott) из университета Аделаиды (University of Adelaide). Не расставив ещё всех точек над i, эти исследователи, как они вычисляют, осознали, в чём заключалась принципиальная неточность предшественников.
Сам Дерек (главная фигура в данном деле) признаёт, что первый намёк на решение парадокса появился не у него, а у доктора наук из Стэнфорда Томаса Ковера (Thomas M. Cover), признанного эксперта по статистике и теории информации. В 2003 году Эбботт трудился в Британии (кстати,на собственной отчизне). И вот как-то, обедая вместе с Ковером, он обсуждал с ним тайную двух конвертов.
Томас и внес предложение уникальную стратегию выигрыша, превосходящую в эффективности кроме того правило «постоянно меняй конверты».
Томас Ковер занимается теорией информации 35 лет. Неудивительно, что кое-какие противоинтуитивные, казалось бы, вещи становятся для него легко понятными и очевидными (фото Stanford University).
Содержится она в следующем. Необходимо поменять либо не поменять конверты в каждом заходе случайным образом, но с возможностью, которая зависит от суммы, замеченной в первом конверте. Другими словами чем меньше сумма в конверте А, тем скорее направляться поменять конверт и напротив, пара солидная сумма в А показывает, что скорее направляться покинуть первый конверт себе.
Тогда, в 2003-м, Дерек посчитал идею собственного коллеги бредом и отказался продумывать такую стратегию. И учёного можно понять: рассудите сами, замеченная сумма не говорит человеку ровным счётом ничего о намерении, условно, ведущего (что раскладывает деньги), так как игрок не знает — в каком по большому счету диапазоне играется его оппонент. Возможно, от 10 центов до 100 американских долларов, быть может, от 5 долларов до ста миллионов.
И замеченные, например, в один раз $25 равнозначно смогут (в рамках всей партии) появляться и сущей мелочью, и самой громадной поставленной на кон суммой. И оттого неясно — стоит ли поменять конверт в данном раунде игры либо нет.
Но, раскинув мозгами, Эбботт заметил за «стратегией Ковера» (так австралийские математики и назвали этот приём) глубочайший философский а также физический суть. «Видимый парадокс появился вследствие того что нельзя избавиться от ощущения, что наблюдение и открытие конверта $10 в действительности ещё не говорит вам ничего. И исходя из этого казалось необычным, что ожидаемое значение вашего выигрыша при смены конверта образовывает $12,5, — пояснил Эбботт. — Но мы растолковываем данный казус с позиций нарушения симметрии.
До открытия конвертов обстановка есть симметричной, исходя из этого не имеет значения, станете вы поменять позже конверт либо нет. Но по окончании того как вы открываете конверт и используете стратегию Ковера, вы нарушаете симметрию (сразу после открытия конверта А оба конверта уже не равноценны), а после этого обмен конвертов разрешает вам взять пользу в долговременном замысле (при солидном числе заходов)».
Всё это напоминает обстановку с «редукцией» кота Шрёдингера к одному из двух состояний (мёртв либо жив), не смотря на то, что до открытия коробки с ядом он будет в суперпозиции вероятных состояний. Это неприятность влияния наблюдателя на итог наблюдения. Ощущаете, что мы подбираемся к неким базам Природы?
Сейчас более чем 20 миллионов компьютерных симуляций, совершённых Макдоннелом и Эбботтом, продемонстрировали, что стратегия Ковера дает возможность приобрести больше денег в игре с конвертами, чем несложный обмен. А ещё, открыли австралийские учёные, предопределённый обмен, в то время, когда игрок выбирает другой конверт лишь в том случае, если замеченная в первом сумма меньше заблаговременно и наугад выбранного им самим (игроком) значения, также трудится. И это так же противоинтуитивно, потому, что о минимальной планке «переключения» знает игрок, но не те, кто кладёт деньги в конверты.
Дабы досконально осознать, как это так получается, возможно взглянуть статью авторов изучения в Proceedings of the Royal Society A. Для нас же принципиально важно неспециализированное объяснение тайны данной игры. И тут нам потребуется обратиться к аналогиям из мира физики и не только.
Первая — «Броуновский храповик» (Brownian ratchet), придуманный известным физиком Ричардом Фейнманом. Это мысленное устройство, являющее собой частный случай не меньше известного Демона Максвелла, отряжённого злостно нарушать второе начало термодинамики, другими словами создавать нужную работу без разности температур двух источников, а только за счёт внутренней (тепловой) энергии единственного объекта (сосуда с газом).
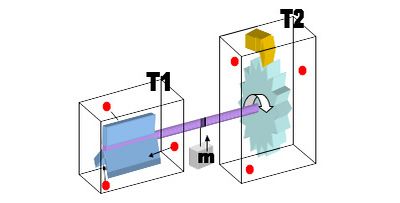
Устройство броуновского храповика (иллюстрация с сайта wikipedia.org).
Устроен и действует фейнмановский храповик так (смотрите рисунок вверху). Имеются две камеры (коробки) с молекулами газа (они продемонстрированы красными кружками). Камеры соединяет миниатюрный вал (трудящийся без трения), на одном финише которого имеется колесо с лопастями (слева), а на противоположном — шестерёнка с храповым механизмом (справа).
Между ними на валу — груз на верёвочке.
Храповик разрешает валу крутиться в одном направлении, но запрещает проворачиваться в другом. Броуновское перемещение молекул в левой камере ведет к хаотичным ударам их по лопастям, но потому, что двигаться лопасти смогут лишь в одну сторону, эти удары неспешно сдвигают колесо, создавая работу по поднятию груза за счёт лишь одной тепловой энергии молекул в первой камере.
«Хитрость с броуновским храповиком содержится в том, что он опять-таки применяет идею разрушения симметрии», — говорит Эбботт. Данное устройство извлекает (помой-му) нужную работу из броуновского перемещения, так же, как игрок «извлекает» увеличение собственного благосостояния из случайного обмена конвертов с нарушенной симметрией (по принципу Ковера). Неравноценная обстановка с возможностями проигрыша и выигрыша в парадоксе конвертов — аналог храповика Фейнмана.
Действительно, физически таковой храповик не существует, даже если бы умелые нанотехнологи его имели возможность выстроить. Из-за чего так — растолковал сам Фейнман. Защёлка храпового механизма должна быть сама небольшой, дабы двигаться в ответ на удары отдельных молекул по лопастям «мельницы».
А потому защёлка будет не меньше прекрасно колебаться и от собственного броуновского перемещения, иногда раскрываясь и разрешая валу сдавать назад.
Фейнман высчитал, что в случае если температуры (Т1 и Т2) в камерах равны — средняя сумма перемещений вперёд будет уравновешена средней суммой перемещений назад, так что сумма будет равна нулю. В случае если же T2 будет меньше Т1, то вправду возможно было бы замечать перемещение данных колёс вперёд. Но в этом случае энергия будет добываться из градиента температур, в согласии с законами физики.
С деньгами всё пара несложнее. Но броуновский храповик оказывает помощь нам осознать принцип работы новой стратегии «обмана» envelopes problem. Ещё увлекательнее аналогия парадокса двух конвертов с другим математическим феноменом — парадоксом Паррондо (Parrondo?s paradox).
Дерек Эбботт (на снимке) считается ведущим исследователем парадокса Паррондо (фото с сайта wikipedia.org).
Звучит он так: «Забрав две (основанные на случае) игры, любая из которых имеет более большие шансы проигрыша, чем победы, возможно выстроить выигрышную стратегию, играясь в эти игры поочерёдно».
Пример тут таков. Допустим, у нас имеется начальный капитал. Потом мы пошагово прибавляем к нему $1 либо вычитаем $1 в зависимости от результата бросания монеток (орёл-решка, предугадали либо нет).
Но монетки не простые, а ассиметричные, так что возможность выпадения одной из сторон хороша от 50%.
Потом, у нас в игре с капиталом имеется в действительности две игры — А и В. Причём в игре А употребляется монета 1 с возможностью отечественного выигрыша 0,5 — e, где е — чуть больше нуля. Ясно, что при солидном числе бросков игра А — неизменно проигрышна для нас.
В игре B имеются две (также несимметричные) монеты (2 и 3), значительно хорошие по возможности отечественного выигрыша друг от друга: к примеру (1/10) — е и (3/4) — е. Помимо этого, заблаговременно вводится наугад выбранное число М. И правило: в случае если текущий капитал кратен М — в данном раунде бросаем монету 2, если не кратен — монету 3.
Всё тот же Эбботт ранее продемонстрировал, что при е = 3 и М = 0,005 игра В — проигрышна равно как и А. Ещё анализ показывает, что возможность применения в очередном раунде «нехорошей» монеты округлённо образовывает 0,6 против 0,4 для «хорошей», из этого и проигрыш в сумме многих попыток. Но вот парадокс: чередование игр А и В разрешает нарастить капитал, не обращая внимания на проигрышность обеих! Да, вовсе не любое чередование ведёт к победе.
А лишь кое-какие комбинации, например, такая — ABBABB и без того потом.
Для рассеивания иллюзии парадокса (а он таков лишь для отечественных поверхностных суждений, на деле же — закономерный результат теории возможности, что продемонстрировали модели с применением сложных правил анализа) направляться осознавать, что в комбинации двух игр обе становятся связанными. Эту практически мистическую сообщение организует именно число М. Так как с его введением движение игры В начинает быть зависимым и от хода игры А. Если бы связи не было — каждая комбинация игр всё равняется приводила бы к проигрышу.
Тут и начинает брезжить свет в проблеме конвертов. Отдельные две игры с монетками являются проигрышными лишь при статистическом распределении результатов всех бросков партии, хорошем от того, что формируется, в то время, когда объединяются эти две игры.
Введение числа М и связи выбора монеты с капиталом (что, один-единственный, значительно уменьшается и возрастает как в игре А, так и в игре В) смещает возможность распределения всех бросков в состояние, при котором появляется хорошее ожидание (результата). А «конверты» и «Паррондо» — сущность родственные парадоксы. Сам Дерек именует решение проблемы двух конвертов прорывом в области анализа парадокса Паррондо (имеющего массу проявлений в жизни).
А основная неточность последовательности предшественников Дерека – высчитывание возможности определённых событий с свободными исходными переменными, каковые свободными на деле не являются.
И тут пора перейти к третьей аналогии — из области финансов. «Volatility pumping» — «Накачка волатильности». Это не мифическая «золотая» программа для игры на бирже, но упрощённая модель, показывающая кое-какие нужные изюминки выигрышной стратегии игры с акциями (товарами, облигациями и другим).
Ясно, что в случае если игрок располагает информацией о получаемых денежных инструментах (состояние компании, судебные дела против её менеджеров, урожай апельсинов в текущем году либо открытие нового месторождения нефти), он может составлять собственный портфель осознанно. Но в случае если ему не известно ничего, не считая текущей цены акции (либо иного приобретения), и того, куда цена на данный момент движется? Ни того, будет ли цена ещё падать, либо позднее начнётся рост?
Ни того — есть ли нынешняя цена большой, минимальной либо позднее будет громадный провал.
Как это похоже на выбор из двух конвертов: больше во втором сумма, чем та, что вы держите в руках, либо меньше? «Насос волатильности» предполагает достаточно хаотичную куплю-продажу активов с маленьким лагом (приобрели дешевле — реализовали дороже), без всякого тревоги о том, взяли ли вы сейчас самую громадную пользу от сделки либо потеряли шанс стать ещё богаче. И это весьма похоже на случайную смену конвертов с некоторым «градиентом» в зависимости от величины замечаемой суммы (снова стратегия Ковера).
Марк Макдоннел (на снимке), как и его напарник по изучению Эбботт, считает, что открытые на протяжении «раскалывания» парадокса двух конвертов закономерности разрешат многие интересные процессы растолковать на единой математической базе, а это даст толчок к новым изучениям в разных сферах – от теории и математики информации конкретно до физики и техники (фото University of South Australia).
И это кроме этого похоже на принцип работы броуновского храповика. И данный же принцип схож с обстановкой, в то время, когда требуется улучшить работу технической совокупности при неполных информации об условиях её работы. «Приводит к удивлению то, что отечественный анализ показывает — неизменно возможно расширить полученный (в игре с конвертами) капитал, применяя способ Ковера, ничего не зная о допустимом пределе суммы в раундах, равно как о статистическом распределении купюр по раундам», — говорит Дерек.
Но возможно ли, допустим, применить следствие из парадокса Паррондо (либо объяснения феномена конвертов) к фондовому рынку, другими словами взять доход, комбинируя акции наподобие игры АВВАВВ? Увы, парадокс требует, дабы доходность как минимум от одного инструмента зависела от величины текущего суммарного капитала (как выбор монеты от кратности уже побеждённой суммы числу М), а это фикция. Либо нет?
Умение рассмотреть подлинные связи между явлениями в том месте, где связей, казалось бы, нет — весьма полезное свойство учёного. Оно оказывает помощь растолковать процессы, выглядящие для поверхностного наблюдателя как немыслимые. Так от пресловутой игры с двумя конвертами ниточка тянется ко множеству вторых областей, в которых проявляется сотрудничество объектов с асимметрией случайности, не имеет значения, порождается ли такая асимметрия храповым механизмом, открытием конверта А либо законами рынка.
И не напрасно, например, Эбботт кроме этого известен как исследователь стохастического резонанса — парадоксального, на первый взгляд, явления усиления нужного (периодического) сигнала в нелинейных совокупностях при добавлении к нему белого шума. Это увлекательное явление сейчас применяется в электронных совокупностях.
Смотрите, какая прекрасная аналогия. Откуда «природа» знает, какую часть импульса усиливать? Это так же неизвестно, как да и то, в каком из двух конвертов солидная сумма денег. Но, при последовательности условий, возможность верного усиления оказывается выше, чем возможность подавления нужной составляющей добавленными помехами.
Так же как возможность выигрыша в «конверты» возможно сознательно повышена, в пику кажущейся неопределённости финала данной несложной игры. Но какие конкретно уж тут игрушки.







