Степан тигунцев о причинах и природе инерции
В собственной прошлой статье я обрисовывал обстоятельство инерции с позиции эфирной догадки тяготения. В настоящей статье употребляются общепринятые в физике понятия, помимо этого, статья дополнена описанием обстоятельств перемещения космических объектов по своим орбитам, обстоятельств вращения их около собственных осей, обстоятельств сил Кориолиса, обстоятельств вращения по инерции волчка и вала.
В данной статье разъясняется, что обстоятельством равномерного и «прямолинейного» перемещения материальных тел в условиях «отсутствия» действия внешних сил, есть сила тяжести, обусловленная гравитационным полем Почвы. Вводная часть была мной достаточно детально изложена, исходя из этого тут не приводится.
Предлагаю следующее уточненное объяснение. Сила тяжести появляется благодаря наличию ускорения свободного падения, вектор которого направлен к центру Почвы вертикально её поверхности.
На тело с массой М действует сила тяжести F, равная произведению массы М на вектор ускорения свободного падения g. Сила F, являясь произведением скалярной величины на векторную, кроме этого есть векторной величиной.
Силе тяжести соответствует однообразный по величине, но противоположно направленный вектор реакции опоры Fr, равный произведению массы М на вектор замедления свободного падения gr, наряду с этим вектор gr равен по модулю и противоположен по направлению вектору g.
В двух, отстоящих друг от друга точках 1 и 2, на горизонтальной для каждой точки поверхности Почвы, на тело с массой М действуют силы тяжести F1 и F2, равные произведению массы М соответственно на вектора ускорений свободного падения g1 и g2, модули которых однообразны.
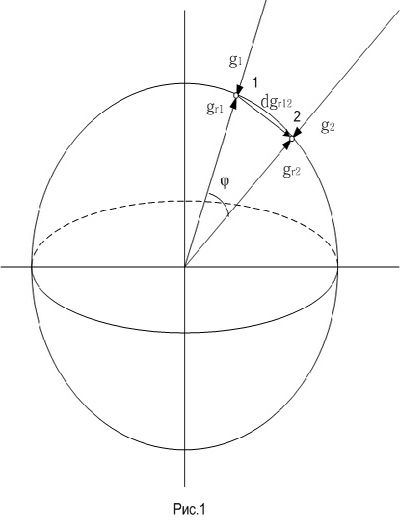
Наряду с этим будем вычислять, что векторы g1 и g2 сходятся в центре Почвы под углом φ (Рис. 1), располагая их в масштабе от поверхности Почвы до её центра (точка O). Векторы сил F1 и F2 кроме этого равны по модулю и сходятся в центре Почвы под углом φ друг к другу (Рис.
2).
Векторы реакций опоры Fr1 и Fr2 приложены в точках 1 и 2 соответственно и равны произведению массы M соответственно на векторы торможений свободного падения gr1 и gr2, модули которых однообразны.
Для наглядности на картинках векторы продемонстрированы под большим углом друг к другу, не смотря на то, что данный угол возможно сколь угодно малым.
Предположим, что тело будет в состоянии равномерного перемещения по «горизонтальной» поверхности Почвы от точки 1 к точке 2 в условиях отсутствия тормозящих воздуха и воздействий поверхности.
Слово «горизонтальной» забрано в кавычки, поскольку горизонтально будет в точке 1, в точке 2, но путь между этими точками есть криволинейным, кроме того на участке длиной в 1 метр, с радиусом кривизны, равном радиусу Почвы.
На это тело при его равномерном перемещении от точки 1 к точке 2 всегда действует сила, равная разности сил Fr2 и Fr1. В соответствии с Рис. 2 переносим начало вектора Fr2 в точку 1. Для двух векторов Fr1 и Fr2, имеющих неспециализированную точку (1) возможно применить правило вычитания векторов (Рис.3).
Вектор ΔF (на рисунке dF), равный разности векторов Fr2 и Fr1, воображает силу, которая, являясь внешней по отношению к телу, действует от точки 1 к точке 2 и снабжает равномерное перемещение тела по «горизонтальной» поверхности Почвы, сколь угодно продолжительно в отсутствии тормозящих обстоятельств.
Так, сила, действующая на тело массой M, определяется формулой:
ΔF = M * (gr2 — gr1). (1)
В выражении (1) разность векторов Δg = (gr2 — gr1)(на Рис. 1 — dg) является ускорением , которое всегда обеспечивает сила ΔF. Под действием данной силы тело будет в состоянии равномерного перемещения со скоростью:
V = |gr2 — gr1| * R / (g * Δt), (2)
Выражение (2) с учётом равенства модулей векторов gr2 и gr1 будет иметь вид:
V = π * R * φ / (Δt* 180),(3)
Где: R — радиус Почвы, g – величина модуля ускорения свободного падения, Δt — отрезок времени, за которое тело проходит со скоростью V расстояние от точки 1 до точки 2, φ – угол в градусах.
Анализ выражения (2) говорит о том, что при Δt -0 приобретаем производную от комплексной переменной gri:
|Δg| / Δt = g * V / R, (4)
Из (4) направляться, что всякому значению скорости равномерного перемещения тела соответствует собственное значение производной от ускорения замедления свободного падения, назовём это значение коэффициентом инерции, его размерность см/сек3.
Из этого направляться, что, обеспечив равномерное перемещение тела по «горизонтальной» поверхности Почвы, мы снабжаем определённую величину коэффициента инерции, которая остаётся постоянной на всём пути перемещения тела, впредь до перемещения по окружности около Почвы, конечно, в условиях отсутствия тормозящих обстоятельств.
Удостоверимся в надежности расчётом справедливость формулы (3). Пускай тело, движущееся равномерно со скоростью V, переместится из точки 1 в точку 2 за 100 сек, наряду с этим угол между векторами ускорений составит 0,001 градуса.
Приобретаем по формуле (3) V = 1,11 м/сек, наряду с этим на тело всегда действует ускорение Δg = 1,11 см/сек2, и тело имеет коэффициент инерции ki= 0,0111 см/сек3. Для первой космической скорости на поверхности Почвы ki = 1,215 см/сек3.
Так, главной и единственной обстоятельством существования равномерного перемещения по «горизонтальной» поверхности есть сила тяжести. Так как в любой точке земного шара имеются вектора ускорения свободного падения, то везде выполняется условие для того чтобы перемещения, независимо от направления на местности.
Сейчас отыщем в памяти формулировку перемещения по инерции как равномерного прямолинейного перемещения тел, происходящего без внешних действий.
Мы убедились, что равномерное перемещение тел происходит в следствии лишь внешних действий, но это перемещение криволинейное (с радиусом кривизны, равным радиусу Почвы), а это значит, что понятие инерции в существующем понимании не применимо.
Это значит, что при прямолинейном перемещении нигде во Вселенной не будетравномерного перемещения тел, происходящего без внешних действий, поскольку все действия на тела во Вселенной имеют радиальный темперамент, другими словами, по законам сферы (все космические объекты, владеющие гравитацией, имеют векторы ускорений свободного падения, строго перпендикулярные собственной поверхности, имеются ввиду сферические объекты с равномерным распределением массы).
Это значит, что инерциальные совокупности отсчёта, в которых свободное тело покоится либо движется равномерно и прямолинейно, без внешних действий таковыми не являются.
Нужно вводить второе понятие, исходя из того, что свободных тел в принципе не существует, исходя из того, что тело может двигаться равномерно лишь криволинейно, наряду с этим лишь под действием сил тяжести другого более массивного тела.
Это значит, что закон инерции в прошлом понимании перестаёт быть тем фундаментом, на котором покоится всё учение о перемещении тел.
Это значит, что инерциальными смогут быть лишь совокупности, в которых присутствует гравитационное действие, а так как в настоящей физической действительности во Вселенной нет места, где бы отсутствовали силы тяготения, то неинерциальных совокупностей в принципе быть неимеетвозможности.
Посмотрим формулировку закона инерции: «Всякое тело сохраняет собственное состояние спокойствия либо равномерного и прямолинейного перемещения, пока неуравновешенные внешние силы не вынудят его поменять это состояние».
Формулировка требует значительной корректировки, из-за которой закон инерции может иметь следующий вид: Всякое тело сохраняет собственное состояние спокойствия либо равномерного и криволинейного перемещения, под действием сил тяготения, пока другие внешние силы не вынудят его поменять это состояние.
В качестве крайне важных следствий изложенных данных исследований направляться следующее:
1. Обстоятельством перемещения космических аппаратов с первой космической скоростью 7,91 км/сек (V = √(g * R), где: g = 9,81 м/сек2, R = (6380 + h) км) около Почвы есть сила тяготения Почвы, наряду с этим аппараты движутся равномерно (относительно поверхности Почвы) в правильном соответствии с новой формулировкой закона инерции.
2. Обстоятельством перемещения Луны с первой космической скоростью 1 км/сек (V = √(g * R), где: g = 0,286 см/сек2, R = (6380 + 384400) км) около Почвы есть сила тяготения Почвы, наряду с этим Луна движется равномерно (относительно поверхности Почвы) в правильном соответствии с новой формулировкой закона инерции.
3. Обстоятельством перемещения планет, каждой со своей первой космической скоростью (Vi = √(gi * Ri), где: gi – ускорение свободного падения Солнца недалеко от орбиты i-ой планеты, Ri — расстояние от Солнца до орбиты i-ой планеты) около Солнца есть сила тяготения Солнца, наряду с этим планеты движутся равномерно (относительно поверхности Солнца) в правильном соответствии с новой формулировкой закона инерции.
4. Неспециализированный вывод – обстоятельством перемещения космических объектов по своим орбитам, каждого со своей первой космической скоростью(Vi = √(gi * Ri), где: gi– ускорение свободного падения центрального объекта недалеко от орбиты космического объекта, Ri — расстояние от центрального объекта до орбиты космического объекта), около центрального объекта есть сила тяготения центрального объекта, наряду с этим космические объекты движутся равномерно (относительно поверхности центрального объекта) в правильном соответствии с новой формулировкой закона инерции.
5. Начальное перемещение космических объектов по своим орбитам появилось из-за неоднородности по массе центрального объекта, что приводило к неравенству модулейускорения свободного падения в двух близлежащих точках орбиты.
6. Обстоятельством равномерного вращения космических объектов около собственных осей есть сила тяготения этих объектов, наряду с этим перемещение с постоянной скоростью происходит в правильном соответствии с новой формулировкой закона инерции.
7. Начальное вращение космических объектов около собственных осей появилось из-за неоднородности по массе объекта, что приводило к неравенству модулей ускорения свободного падения в двух близлежащих точках поверхности объектов.
Потом разглядим явления, которые связаны с действием сил тяжести на тела, каковые будут в состоянии равномерного перемещения на вращающемся космическом объекте, к примеру эффект Кориолиса на поверхности Почвы.
В общепринятом понимании под силой Кориолиса либо кориолисовой силой инерции знают силу инерции, которая появляется при перемещении тела довольно вращающейся совокупности отсчёта.
Разглядим механизм происхождения данной силы для случая перемещения тела по меридиану в северном полушарии (Рис. 4).
Как установили выше, на тело при его равномерном перемещении от точки 1 к точке 2 всегда действует сила ΔF, равная разности сил Fr2 и Fr1в соответствии с (1).
Где разность векторов Δg = (gr2 — gr1) является ускорением , которое всегда обеспечивает сила ΔF.
Под действием данной силы тело в отсутствие тормозящих действий будет в состоянии равномерного перемещения со скоростью, определяемой по (2).
В случае если тело будет в состоянии равномерного перемещения с Юга на Север по поверхности Почвы, которая вращается с Запада на Восток (слева направо на Рис. 4), то сила ΔF будет стремиться сохранить существующее сейчас направление перемещения.
Наряду с этим поверхность Почвы будет стараться переместить тело в направлении собственного вращения. поверхности Земли и Дальнейшее взаимодействие тела будет зависеть от характера тела.
В случае если тело – шар, то он будет отклоняться влево от предполагаемой траектории Юг-Север, в случае если это вода в реке, то она будет кроме этого отклоняться влево в рамках берегов, другими словами, будет оказывать большее действие на западный берег, в случае если это поток воздуха, то он кроме этого будет отклоняться влево.
На Рис. 4 продемонстрировано вероятное положение векторов gr2 и gr1 в точках 2 и 1, расположенных на меридиане для случая не вращения Почвы.
За время Δt точки 2 и 1 вместе с поверхностью Почвы окажутся в точках 4 и 3 соответственно, которым соответствует положение векторов gr4 и gr3.
Но тело (к примеру, шар) наряду с этим окажется в точке 4’, в соответствии с траекторией, продемонстрированной жирной кривой линией. Данной точке соответствует вектор g?r4.Разность векторов g?r4 — gr4 представляет собой Сила Кориолиса gk.
Соответственно, Кориолисово ускорение определится выражением:
Fk = М * gk, (5)
При таком характере перемещения на тело будет всегда действовать сила Fc, направление которой отличается от ее начального направления, равная сумме сил ΔF и Fk, которая создаёт ускорение gс.
Потом разглядим обстоятельства инерции тел, вращающихся в условиях гравитационного действия другого тела, другими словами, обстоятельства инерции вращающихся тел, имеющих вертикальную либо горизонтальную оси вращения.
На рис. 5 изображена схема размещения тела, имеющего вертикальную ось вращения (волчок), вращающегося с постоянной угловой скоростью ω, продемонстрировано положение векторов замедления свободного падения gr2 и gr1, и вектора ускорения волчка — Δg12, которое всегда обеспечивает сила ΔF12.
Однако здесь направляться ещё учесть, что с противоположной (по диаметру) стороны волчка сила ΔF34 снабжает ускорение Δg34. Наряду с этим коэффициент инерции кольцевого элемента волчка с радиусом Rv определяется выражением:
|Δg| / Δt = g * ω * RV / R, (6)
На рис. 6 изображена схема размещения тела, имеющего горизонтальную ось вращения (вал), вращающегося с постоянной угловой скоростью ω, продемонстрировано положение векторов замедления свободного падения gr2 и gr1, вектора ускорения Δg12, которое всегда обеспечивает сила ΔF12, положение векторов замедления свободного падения gr4 и gr3, и вектора ускорения направляться;g34, которое всегда обеспечивает сила ΔF34.
В общем, приобретаем схему, подобную волчку, но, тут направляться подчернуть, что векторы gr2 и gr1 не равны по модулю.
Наряду с этим коэффициент инерции кольцевого элемента вала с радиусом Rv приближенно возможно выяснить по выражению (6), где g и R выяснены относительно оси вала.
При размещения оси вращающегося тела под любым вторым углом к поверхности Почвы ответ приобретаем в общем виде:
Δg = dR/dS * d2S/dt2 + dR2/dS2 * (dS/dt)2, (7)
направляться подчернуть, что по формуле (7) возможно кроме этого рассчитывать скорости ускоренного перемещения.
Вывод: предложенное объяснение обстоятельств происхождения инерции разрешает полностью обрисовать динамику перемещения тел.
Связаться со Степаном Георгиевичем Тигунцевым возможно по адресу stiguncev@yandex.ru.