Геометрические построения при выполнении разметки плоских поверхностей
При плоскостной разметке приходится делать разнообразные построения: дробить прямые линии на равные части, проводить перпендикулярные и параллельные линии, строить углы, дробить окружность и углы на равные части и т. д. Указанные и другие построения слесарь обязан мочь делать скоро и совершенно верно, а для этого требуется прочно усвоить элементы черчения.
деление и Нанесение отрезков их на равные части. При откладывании размеров на риске по измерительной линейке вероятны неточности, каковые смогут сказаться и на точности разметки. Дабы избежать неточностей, направляться предварительно в точке, от которой необходимо откладывать размер, нанести поверхностный керн, после этого одну ножку циркуля, установленного на нужный размер, поставить в керн, а второй делать засечку на риске. В точке пересечения засечки с риской снова наносят керн, а после этого откладывают следующий размер обрисованным методом и т. д.
Чтобы поделить заданный отрезок АВ на две равные части, произвольным радиусом, громадным половины отрезка, выполняют две дуги из точек А и В, через точки а пересечения этих дуг выполняют перпендикуляр, что и поделит отрезок совершенно верно пополам. В случае если отрезок АВ большой и дуги, совершённые из крайних точек, пересекаются за пределами размечаемой подробности, поступают так: сначала из точек А и В произвольным радиусом делают две однообразные засечки в точках k1 и k2, после этого из этих точек выполняют две дуги, каковые пересекаются в пределах размечаемой плоскости в точках Ь.
Деление отрезков на 4, 8, 16 и т. д. равных частей создают вышеуказанным методом: сперва дробят отрезок пополам, после этого каждую половину снова пополам и т. д.
Разметка параллельных, перпендикулярных и наклонных рисок. Данный вид разметки производится посредством масштабной линейки, разметочного циркуля и угольника.
Для разметки параллельных рисок масштабной линейкой нужно последнюю наложить на размечаемую поверхность заготовки так, дабы деление отсчитанного размера совпало с линией либо кромкой торца заготовки, принятой за разметочную базу. После этого по нулевому делению линейки наносят чертилкой метку. Такие метки засекают с двух сторон заготовки и соединяют их прямой линией.
В случае если параллельные линии возможно совершить посредством угольника с полкой, то засекают лишь одну метку, что существенно активизирует разметку.
Разметку линий посредством разметочного циркуля возможно делать и без того: за разметочную базу принимают обработанные стороны заготовки. Ножки циркуля устанавливают по линейке на нужный размер и одной из них ведут по краю заготовки, а острием второй наносят параллельно ему засечки либо дуги, каковые соединяют прямой. Данный метод особенно эргономичен при разметке центров отверстий на плоскости.
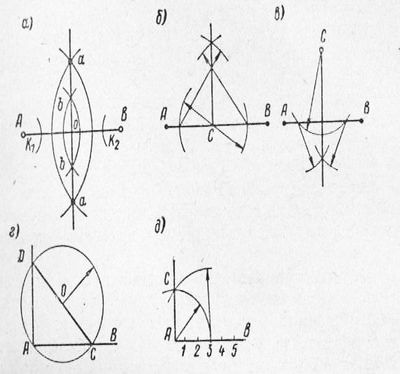
Рис. 1. Несложные построения при разметке: а — деление отрезка на равные части; б—проведение перпендикуляра к прямой АВ в точке С на прямой; в—проведение перпендикуляра к прямой АВ из точки С, расположенной вне прямой; г и б—проведение перпендикуляра к прямой АВ
Построение перпендикулярных рисок геометрическим методом производится посредством циркуля и линейки (рис. 1, б, в, г, д). Разметка перпендикулярных рисок при помощи угольника с полкой от разметочной плиты делается так.
Заготовку устанавливают на углу разметочной плиты. После этого, прикладывая угольник к боковой поверхности п разметочной плиты, выполняют на плоскости заготовки риску I—I. Затем угольник прикладывают полкой к боковой поверхности т разметочной плиты, как это продемонстрировано штриховыми линиями.
Так как боковые поверхности плиты перпендикулярны друг другу и верхней плоскости плиты, то, прижимая полку угольника к боковой поверхности т, через любую точку заготовки возможно совершить риску II—II, перпендикулярную ранее совершённой риске I—I. Приемы нанесения рисок посредством угольника с полкой от обработанных кромок подробности продемонстрированы на рис. 2, ж.
Рис. 2. Методы разметки параллельных рисок (а, б, в, г, д) и перпендикулярных рисок при помощи угольника от разметочной плиты (е) и от обработанных кромок подробности (ж)
Положение наклонной линии на чертеже возможно выяснено соответствующей надписью, углом наклона либо размерами.
В первом случае наклонная линия задана надписью: «Уклон 1 :5». Это указывает, что на каждые 5 мм длины (по горизонтали) наклонная линия поднимается (либо опускается) на 1 мм. Для примера на рис. 48, а приведено такое построение наклонной линии: на прямой АВ откладывают отрезок 50 мм, после этого из точки С выполняют перпендикуляр, на котором откладывают 10 мм (отрезок CD); прямая, проходящая через точки AD, и будет иметь уклон 1 :5.
Для окончания разметки необходимо на прямой АВ отложить отрезок длиной 100 мм и из точки В совершить перпендикуляр до пересечения с продолжением наклонной линии AD.
Рис. 3. Разметка положения наклонных рисок (а, б, в); деление углов на равные части (г. д); построение сопряжений (е, ж, з. и)
Во втором случае наклонная прямая задана на чертеже углом наклона а=15°. Разметку в этом случае создают посредством малки, установленной по транспортиру, либо угломера.
В третьем случае для разметки наклонной риски нет необходимости прибегать к помощи особых инструментов либо создавать какие-либо дополнительные вычисления. Разметку ведут простым методом: сперва откладывают отрезок длиной 150 мм, в конце которого строят перпендикуляр. На перпендикуляре откладывают 40 мм.
Соединив финиши отрезков, приобретают искомую наклонную риску.
Дабы поделить угол на две равные части, из вершины Л дугой произвольного радиуса делают засечки на сторонах угла. Из взятых точек В и С как из центров выполняют дуги радиусом, громадным половины дуги ВС, а точку пересечения дуг D соединяют с вершиной угла А. Полученная прямая AD разделяет угол ВАС совершенно верно пополам.
При делении прямого угла на три равные части из вершины А произвольным радиусом R выполняют дугу до пересечения со стороной угла; из точек пересечения В и С дугами того же радиуса пересекают дугу ВС в точках D и Е, после этого соединяют точки пересечения дуг D и Е с вершиной угла А. Прямые DA и ЕА дробят прямой угол на три равные части.
Разметка контуров, складывающихся из сопряженных кривых и прямых линий. Сечения поверхностей, определяющих форму подробностей автомобилей, как правило образованы плавными сопряжениями двух прямых, прямой с дугой, окружности с дугами двух радиусов и т.д. В заводской практике пользуются двумя методами разметки плавных сопряжений: способом попыток (приближенный метод) и при помощи геометрических построений (более надежный метод).
Плавный переход между двумя дугами окружностей достигается лишь тогда, в то время, когда точка сопряжения их будет на прямой, соединяющей центры О и О! окружностей этих дуг. При внешнем касании расстояние между центрами’дуг должно равняться сумме их радиусов, а при внутреннем касании — разности.
Рис. 4. Разметка дуги, касающейся двух прямых, образующих угол (а); разметка сопряжения двух окружностей с дугой заданного радиуса (б)\ деление окружности на равные части (в)
Разметку дуги данного радиуса R, касательной к двум данным прямым, образующим произвольный угол (рис. 4,а), делают так: на расстоянии R параллельно данным прямым АВ и ВС выполняют две вспомогательные прямые. Пересечение этих прямых даст искомый центр О, из которого выполняют дугу.
Точками каса-нпя (сопряжения) являются точки Е и Е1 (основания перпендикуляров, опущенных из центра О на заданные прямые).
Деление окружности на равные части.
Поделить окружность на равные части возможно тремя методами:
1) геометрическим построением, т. е. графически;
2) применяя коэффициенты, забранные из особых таблиц;
3) при помощи особых разметочных приспособлений.
Геометрические построения. На рис. 49,в приведено графическое построение, при помощи которого возможно поделить заданную окружность на произвольное число п равных частей, к примеру «=11.
Проводим взаимно перпендикулярные диаметры АВ и ЕС заданной окружности. Из точки А откладываем произвольные, но равные друг другу отрезки, количество которых равняется заданному числу п делений окружности. Крайнюю точку М последнего отрезка соединяем прямой с точкой В. Через точку, отстоящую от точки М на два деления, т. е. через точку 9, проводим прямую, параллельную ВМ, до пересечения ее с АВ в точке а.
Деление окружности на любое число равных частей возможно создавать посредством значений коэффициентов, указанных в табл. 3. В первой графе табл. 3 указаны числа, на каковые нужно поделить окружность.
Во второй графе указан коэффициент, на что направляться умножить диаметр делимой окружности, дабы выяснить длину хорды, равную стороне соответственного вписанного многоугольника.
Установить циркуль совершенно верно на размер 20,79 мм весьма тяжело (в большинстве случаев циркуль возможно установить с точностью, не превышающей 0,1 мм). Следовательно, в случае если в этом случае циркуль будет установлен на размер 20,7 мм, то при нанесении 15 делений пятнадцатое деление окажется на 1,3 мм больше вторых делений. К этому смогут прибавиться еще неточности на протяжении откладывания делений и в итоге окажется, что последнее, пятнадцатое деление на заметную величину отклонится от остальных делений.
Дабы избежать накопления неточностей при откладывании делений, прибегают к следующим приемам.
Выяснив при помощи таблицы длину одного деления, сходу не дробят окружность на 15 равных частей. Сперва простым методом дробят окружность на три равные части, находят точки А, В и С, а после этого, установив циркуль с максимальной точностью на подсчитанную длину 20,79 мм, дробят раздельно каждую часть окружности АВ, ВС и СА на пять частей. При таком методе деления неточность значительно уменьшается в 3 раза.
Еще меньшая неточность при делении окружности окажется, в случае если мы вместо циркуля будем пользоваться разметочным штангенциркулем.
Использование особых разметочных приспособлений при делении окружностей на равные части освобождает слесаря либо разметчика от запасных графических построений либо расчетов посредством таблиц.
На рис. 50, а продемонстрировано простейшее приспособление этого типа, так называемая челябинская линейка, складывающаяся из двух линеек 1 и 2, соединенных шарниром 3. На линейках нанесены неравномерные шкалы с маркировкой точек 5, R, 7,8,9 и т. д.
Для получения величины хорды, дробящей окружность, к примеру, на пять равных частей, раздвигают этого 1 приспособления 2 и линейки так, дабы расстояние между точками R — R равнялось радиусу заданной окружности. Тогда расстояние между точками 5 — 5 дает величину искомой хорды. При делении окружности этого же радиуса на семь частей нужно забрать расстояние между точками 7—7 и т. д.
Для определения хорд, соответствующих заданным центральным углам, на базе челябинской линейки создан особый прибор уникальной конструкции (рис. 50,6). В таком приборе любая линейка 1 и 2 имеет по две шкалы — одну равномерную (диаметров), другую убывающую (радиусов). Градусный сектор 3 связан без движений с линейкой 2. На линейке 1 укреплен нониус для правильного отсчета углов.
Таковой прибор универсален и если сравнивать с челябинской линейкой не усложнен. Устройства этого типа продемонстрировали такую точность в работе, что практически отпала необходимость в последующей «разброске» неувязки.
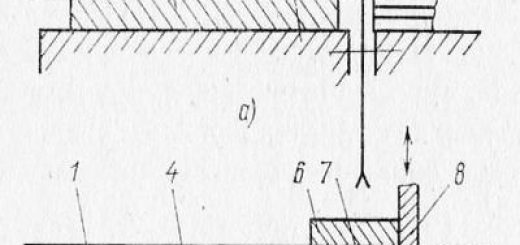
Разметка центров круглых тел, дуг и окружностей. Центр на торцах цилиндрических подробностей находят при помощи циркуля либо угольника-центроискателя, как это продемонстрировано на рис. 51, а, б.
При разметке круглых фланцев, дисков и им аналогичных подробностей, где уже имеются готовые отверстия, центр которых малоизвестен, рекомендуется пользоваться одним из следующих способов геометрических построений. В отверстие, подлежащее разметке, забивают брусок из дерева (рис. 51,в).
После этого на краю отверстия произвольно намечают три точки А, В, С и из них как из центров засекают дуги до пересечения в точках 1, 2, 3 и 4. Через полученные наряду с этим точки пересечения 1, 2, 3 и 4 посредством линейки выполняют прямые линии. Пересечение этих линий и выяснит центр отверстия.
Рис. 5. Особое разметочное приспособление— челябинская линейка
Эта же задача возможно решена и вторым методом. На заданной окружности (либо дуге) выбирают две произвольные точки А и В, каковые легко накернивают. Из этих точек произвольным радиусом делают засечки.
Точки аи а2, Ьх и Ь2 пересечения засечек с заданной окружностью (либо дугой) накернивают. После этого из этих точек радиусом, приблизительно равным 2/3 длины хорд ахо.2 и Ь{Ь2, делают засечки, каковые пересекутся в точках С и D. Потом через точки Л и С, и через точки В и D выполняют прямые, каковые пересекутся в искомом центре — точке О.
Развертка несложных тел. Слесарю довольно часто приходится изготовлять изделия из листового и профильного материала, каковые имеют форму цилиндра, конуса, куба и т. д. Исходя из этого при разметке таких заготовок нужно мочь верно выбрать их настоящие размеры, дабы размеченная заготовка по окончании вырезки и эластичны приняла требуемые по чертежу размеры и форму. Для нахождения настоящих размеров заготовок необходимо произвести так именуемую развертку поверхностей на плоскости.
Рис. 6. Разметка центров: а — циркулем; б — угольииком-центроискателем; в и г—нахождение центров отверстий геометрическим методом
Развертка цилиндра представляется в виде прямоугольника с высотой, равной высоте Н цилиндра, и длиной, равной длине окружности основания цилиндра. Протяженность окружности цилиндра определяется умножением диаметра основания цилиндра на 3,14, т. е. L = nD. Чтобы получить полную развертку (на листовом материале), к размерам развертки нужно добавить припуск на соединение с загибом (соединение на фальц) и на отбортовку.
Рис. 7. Развертка цилиндра (а) и конуса (б)