Иван алюминин приглашает к дискуссии о математике и политике
Математику именуют царицей наук. Желаем мы того либо нет, любой объект либо явление окружающего мира возможно обрисовать количественно, используя математические закономерности. Развитие вычислительной техники, а с ней прикладного применения булевой алгебры, наглядное тому подтверждение.
Современные компьютерные игры уже наталкивают на идея, что люди и окружающая действительность – «матричная» модель, придуманная Кем-то. Однако, важное значение для жизни людей имеет вторая область знаний – политика, которая далеко не всегда дружит с математикой, а, следовательно — со здравым смыслом.
Математика нейтральна неизменно. Политика — фактически неизменно предвзята и коррелированна такими иррациональными явлениями, как нравственность и мораль. Не было бы в этом ничего нехорошего, и всё было бы рационально, если бы не двойные, тройные и иные стандарты названных явлений.
Одно да и то же явление различные политики смогут оценить диаметрально противоположно. Всевышний бы с ними, убогими, если бы они не навязывали собственных догм остальному населению и не сталкивали людей между собой, обычно в кровавых конфликтах.
По плану, настоящая статья аполитична. Она не навязывает чего-либо, а приглашает к дискуссии на политические темы с применением необычного подхода: говорить прямо и отвлечься от их общепринятых определений.
К примеру, отнимать и дробить, в обиходе — очень плохо окрашенные действия. В математике они не имеют окраски, так же, как прибавлять и умножать. В повседневной жизни мы не в состоянии уйти от субъективизма и эмоций, так давайте хоть тут попытаемся встать над проблемами, а не плестись у них в хвосте.
Согласно точки зрения автора, при активном дискуссии это может оказаться весьма интересно и познавательно. И не беда, в случае если кто-то привнесёт-таки ко мне морально-нравственную либо иную окраску, обостряя дискуссию.
Неравенство-математический символ
Традиционно применяемый для изучения общества подход – исторический. Не будем его опровергать, но попытаемся притянуть ко мне математику. Не поразмыслите, что потом будет предложен итог фундаментального изучения.
Это один из бессчётных образчиков нетрадиционного подхода.
Разглядим уровни социального достатка населения в неком обществе графически, с применением элементов математики. На рис. 1 оси ординат соответствует полный суммарный материальный достаток, дешёвый количеству людей n, отсчитываемых по оси абсцисс.
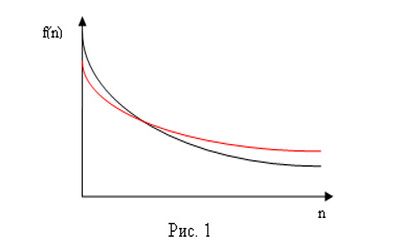
Для пояснения указанной зависимости приведём пара формул. В любом настоящем обществе достаточно мало людей, владеющих большим достатком, и довольно много – ограничивающихся каким-то минимумом. Средний достаток характерен какому-то среднему количеству людей. Иными словами неспециализированное народонаселение разглядываемого общества возможно выразить формулой:
Соответственно, совокупный национальный продукт выразится:
Не нужно обращать внимание на то, что на графике нарисовано общество, близкое к коммунистическому. В любом настоящем обществе достаток самый богатых людей в тысячи раз превышает достаток самый бедных.
Будем вычислять, что ось ординат имеет логарифмическую шкалу. Так компактнее и нагляднее. Принципиально важно осознать кроме этого да и то, что на рисунке изображён как раз график, а не зависимость.
Значение f(n) в каждой его точке – величина статистическая, искусственно приведённая к значению n. А вот в случае если мы сможем доказать как раз зависимость этих размеров, тогда возможно будет сделать и выводы.
Что, фактически, даёт данный график? Во-первых, в случае если тёмная кривая соответствует настоящему распределению материальных благ, то красная кривая определяет допустимый предел этого распределения в данном обществе.
В разглядываемом случае в обществе сложилась достаточно страшная, но не критическая обстановка: большинство людей вычисляет собственный достаток недопустимо низким, но самый богатые уверены в том, что имели возможность бы и поделиться доходами.
Вычислив соответствующие суммы, возможно выяснить, имеются ли в обществе объективные возможности для предотвращения социального взрыва чисто экономическими способами.
Под вторыми способами подразумеваются, в первую очередь, идеологические и репрессивные действия власти, талантливые до определённых пределов понизить красную кривую на тех либо иных участках.
Во-вторых, не нужно иметь развитой фантазии, дабы, поупражнявшись с двумя цветными карандашами, изобразить экономическую обстановку в любом настоящем обществе в историческом контексте. Согласитесь, уже это сэкономит бумагу, если сравнивать с классическим описанием.
В-третьих, в случае если вычислять, что приведённый график есть следствием неких причин, то мы можем приблизиться и к доказательству зависимости. Каковы же эти причины?
Не будем углубляться в первобытные столетия, остановимся на классовых обществах. Непременно, представители господствующих классов постоянно имеют громадные возможностей по достижению материального и иного благосостояния, чем представители низов.
Иными словами, люди имеют различные стартовые возможности. Либо, выражаясь математически, возможность (Р) преумножения и сохранения имеющегося, у верхов существенно выше, чем у низов.
Принимая к сведенью, что борьба, в плане присвоения чужого, в ранних классовых обществах носила весьма твёрдый темперамент, возможно сказать уже о зависимости P(n), которая графически весьма похожа на f(n) с рис. 1.
Лишь в безотносительном выражении, возможно, более крутая. Корреляция f(n) возможностью P(n) очевидна и с доказательством до тех пор пока, наподобие всё в порядке.
По мере развития цивилизации всё большее и большее значение стали приобретать интеллектуальные качества человека, в плане обеспечения собственного достатка. Кое-где уже начали сказать об «обществе равных возможностей».
Создатель не согласен с этим и уверен в том, что кривая P(n) ещё далеко не «выпрямилась» кроме того в самых успешных государствах Запада. Непременно, она стала более пологой.
Кроме того, в случае если создатель неправ, что это меняет? Каково распределение интеллектуальных качеств в любом обществе? Да совершенно верно такое же, как на рис.
1. Гениев очень мало, мало и просто гениальных. Талантливых больше, а «троечников» — много.
Само собой разумеется, никакой гений не может быть в тысячу раз «умней» среднестатистического человека. Да и чем это измерить? Да и сами слова «умней» либо «глупей» очень условны.
Забрать выдающегося спортсмена, что едва-едва осилил школу . Что возможно сообщить о его интеллекте? По всей видимости, лишь то, что ему хватило ума заняться своим делом и достигнуть, материальном замысле того, чего не каждый академик достигает.
Чего греха таить, далеко не всем из нас для того чтобы ума хватает, не смотря на то, что и высшее образование у большинства не одно.
Так или иначе, но тяжело не дать согласие с тем, что кривая f(n) на данный момент очень сильно коррелируется распределением интеллекта в обществе. Не в таковой мере, как P(n) раньше, но однако.
Появляется вопрос, отчего же на фоне понижения крутизны P(n) и низкой, a priori, крутизны распределения интеллекта, кривая f(n) остается достаточно крутой. Ответ содержится в нравственности и морали, с которых мы и начали.
Распределение морально-нравственных качеств в обществе имеет совсем второй темперамент. Приблизительно оно выглядит, как на рис. 2.
Вправду, отъявленных подлецов в любом обществе мало. Мало и нравственных личностей. Большинство людей по своим качествам находятся между ними.
Одни более честные, но время от времени поддаются слабостям. Другие более лукавы, но способны на добропорядочный поступок. Основное, что по-любому, поменять эту зависимость в корне не удастся.
Подтверждение этому вся история цивилизации. Нет, по мере развития человечества и его моральных сокровищ, изображённый полуэллипс приподнялся над осью абсцисс.
Возможно, пара сплющился. Возможно сказать кроме того о его искривлении, но сущность остаётся прошлой.
Наконец, самое спорное. Никаких математических доказательств, не считая эмпирической проверки у автора нет. Но он смеет утверждать, что:
Правильнее, следовало бы написать не равенство, а пропорциональность, тогда бы отпала необходимость в труднообъяснимом коэффициенте на данный момент.
Обстоятельство очевидна, создатель не отыскал во встроенном редакторе формул соответствующий значок. Однако, это не помешает проверить формулу и сделать выводы. А они элементарны.
При равных стартовых возможностях, человек, не обременяющий себя нравственностью и моралью, неизменно способен достигнуть в материальном замысле большего, чем обременённый.
Чем ниже он морально, тем выше его шансы. Как на данный момент говорят, «кинуть» возможно любого компаньона, а также — и приятеля детства. А таковой фокус: выпросить денег взаймы, а позже убить кредитора, дабы не отдавать долг?
Это Раскольников мучался, но из нищеты так и не вылез. Иные времена – иные нравы.
направляться подчернуть, что в данной формуле P(n) включает и интеллектуальные качества. Ясно, что умный мошенник постоянно достигнет большего, чем умный трудоголик.
Кое-какие выводы из всего
Во-первых, социального равенства в людской обществе не было, нет и быть неимеетвозможности, как вечного двигателя, к примеру.
Кое-какие утверждают: правда жизни заключена в том, что одни люди охотники, другие – дичь. Эта идея различными авторами интерпретируется различными эпитетами, но по собственной сути она, к сожалению, верна.
А раз так, то на человечность, права человека, народовластие, да и по большому счету на правомерность возможно взглянуть совсем с вторых позиций, чем это принято.
Уже на данный момент возможно додуматься, что за перечисленными высокими понятиями обычно кроются инструменты, разрешающие одним свежевать вторых. Но в отличие от средних столетий, в то время, когда вещи ещё именовали собственными именами, это делается как бы из высоких побуждений.
Во-вторых, не нужно принимать изложенное, как траурный марш на могиле общечеловеческих сокровищ. Это не призыв к нигилизму. Это попытка назвать опять вещи собственными именами.
Лишь при таком подходе возможно отыскать рациональное зерно и поставить вещи с головы на ноги, по крайней мере, в собственной голове.
Создатель готов продолжить публикации, раскрывая обозначенные темы в разглядываемом контексте. Нет уверенности и в том, что дискуссия станет довольно популярной. Но поживём – увидим.







