Константин агафонов о магнитной природе тяготения
В базе ОТО лежит догадка о геометрической природе поля тяготения, в котором перемещение тел осуществляется по инерции на протяжении геодезических. Это поле объединяется с физическим полем сил инерции в единое гравитационное поле, благодаря чему закон глобального тяготения Ньютона входит в уравнения Эйнштейна в качестве приближённого, а новая теория тяготения удовлетворяет принципу соответствия.
Но, как показывает опыт развития ТО Эйнштейна, геометрическое представление физических полей ведет к неразрешимому внутреннему несоответствию, обусловленному чуждостью для неё (геометрии) базисных физических понятий — силы, энергии и массы.
Оказывается, в случае если мы обрисовываем свойства настоящего мира геометрией Евклида, то приходим к понятиям однородного и изотропного пространства-времени, в котором выполняются фундаментальные законы настоящего мира — законы сохранения.
Наряду с этим приходится оперировать инерциальными совокупностями отсчёта, которым в реальности нет места. Наоборот, неевклидова геометрия искривлённого пространства-времени разрешает оперировать «настоящими» неинерциальными совокупностями отсчёта, но ведет к нарушению законов сохранения в таком мире благодаря неоднородности и неизотропности неоднородности и пространства времени [1].
Данный и другие недочёты теории тяготения устраняются, в случае если формирование геометрической (сферической) структуры пространства-времени вблизи массивного тела приписать его магнитному полю.
В этом случае преемственность с теорией тяготения Ньютона обеспечивается введением в исходные уравнения закона Кулона для магнитных сил, сходного с законом тяготения Ньютона.
Наряду с этим неприятность чёрных дыр остаётся открытой благодаря принципиального отсутствия сингулярностей в процессах магнитного сотрудничества тел, а вместо гравитационных волн теория обязана предвещать классическое электромагнитное излучение как следствие трансформации во времени магнитных полей взаимодействующих космических весов.
Уравнение перемещения частицы в полевой форме
Будем исходить из хорошего определения вакуума как полевой трактовки и абсолютной пустоты физических сотрудничеств материальных тел. Тогда перемещение частицы m по инерции в поле тяготения тяжёлого тела М (рис. 1) возможно обрисовать обобщённым уравнением Лоренца:
(1а)+ mdu/dt = 0.
Тут второе слагаемое характеризует силу инерции частицы при центростремительном ускорении du/dt, первое задаёт «упругие» особенности суммарного силового магнитного центрального тела и поля частицы: K – модуль упругости либо жёсткость поля, u/c – относительная деформация его, u – скорость частицы, c – скорость деформирования силового поля либо скорость света. Комбинация этих сил и воспринимается нами как сила гравитации F.
Тогда оказывается, что свободная частица (M = 0) в соответствии с уравнению (1а) взаимодействует с довольно не сильный собственным силовым полем и движется по винтовой траектории, которая возможно выстроена при учёте следующей эквивалентной формы исходного уравнения:
(1б) [iK, iu/c] + mdu/dt = 0.
Тут i — мнимая единица, умножение на которую свидетельствует поворот вектора на прямой угол в направлении перемещения частицы [2]. Схема перемещения и действующие на частицу силы для этого случая представлены на рис. 2.
Из рис. 2, а видно, что вращение свободной частицы со скоростью iu ведет к происхождению радиальной вращающейся силы [iK, iu/c], обусловленной упругими особенностями K собственного поля. Эта сила уравновешивает радиальную (центробежную) составляющую силы инерции, обусловленную центростремительным ускорением частицы:
(2) [iK, iu/c] = [m(iu)2/r]r0.
А из рис. 2, б направляться, что поступательное перемещение частицы порождает циркуляцию силового вектора , что уравновешивает силу инерции частицы в направлении касательной к окружности вращения:
(3) (iu/c)K = mdu/dt,
где iu = – rw.
Указанные составляющие полной упругой силы и снабжают самоподдержание режима свободного винтового перемещения частицы.
Поворачивающийся комплексный вектор
Уравнения (1а) и (1б), будучи уравнениями гармонических колебаний, определяют некий поворачивающийся комплексный вектор (подробности на отечественном сайте и в работе [3]), талантливый задать на плоскости круговое векторное поле, а в пространстве — сферическое.
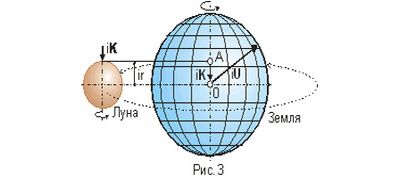
И в этом случае для описания тяготения нет потребности прибегать к сложному математическому аппарату тензорного исчисления (ОТО Эйнштейна). Отечественная задача радикально упрощается: нужно отыскать поворачивающийся комплексный вектор силы либо энергии iU (рис. 3), характеризующий гравитационное поле в общем случае.
Для осевой составляющей жёсткости поля (рис. 2) имеем:
(4) iK = – iLc/(ir)2 = – mciH/(ir)2,
где iH = iL/m = – ru = Const — удельный (на единицу массы) момент импульса iL самовращающейся частицы.
Видно, что сила (4) распространяется на прилегающее пространство, убывая по величине обратно пропорционально квадрату расстояния ir от плоскости вращения частицы.
Это согласуется с опытами по обратимому магнитомеханическому эффекту: вращающаяся инертная масса порождает осесимметричное магнитное поле, превращая эту массу в магнит; и напротив, при внесении незаряженного тела в магнитное поле оно начинает медлительно вращаться.
По-видимому, этот эффект и экспериментальный закон Кулона для магнитных сил обнаруживает соотношение (4).
На рис. 3 приведена схема формирования поля тяготения на поверхности Луны, вращающейся около Почвы и по большей части формирующей магнитное поле отечественной планеты. Тут представлена сила (4), влияющая на полюсы Луны и обусловленная притяжением магнитных центров О Луны и А частиц поверхности её полюсов.
Эта сила задаёт поворачивающийся комплексный вектор, что и формирует сферическое поле тяготения частиц на поверхности отечественного естественного спутника. По такой же схеме формируется поле тяготения Почвы: за счёт вращающегося комплексного вектора, расположенного в центре вращения отечественной планеты (в недрах Солнца) и влияющего на её полюса.
Закон глобального тяготения Ньютона
Полная энергия совокупности частица-поле при дорелятивистских скоростях определяется суммой внутренней m0c2 = Const и кинетической m0u2/2 = Var энергий частицы.
По логике вещей, при захвате свободной частицы тяжёлым телом (рис. 4, частица в положении 1) первая обязана сохраниться количественно и как следует, а вторая преобразоваться в энергию связи с центральным телом.
Наряду с этим частица переходит с орбиты громадного радиуса самовращения, обусловленной довольно малой жёсткостью собственного силового поля, на орбиту с меньшим радиусом самовращения, задаваемую более твёрдым силовым полем захватывающего центрального тела.
В общем случае в ходе захвата центр О самовращения частицы не сходится с центром тела M, и по завершении процесса захвата он сам начинает вращаться около центра тяжёлого тела.
Результатом сложения указанных двух видов вращения — самовращения центра и движения частицы O — выясняется вращение первой около второго по замкнутой спиральной траектории (рис. 4, частица в положении 2), включающей годовое (около центрального тела) и дневное (около оси спирали) вращение частицы-планеты.
Так, попадая в поле центральной силы, частица двигаетсяпо спиральной траектории, обрисовываемой теми же уравнениями перемещения (2) и (3) при возросшей суммарной жёсткости K силового поля.
Первое уравнение ведет к уравнению баланса энергии годового вращения связанной частицы-планеты:
U = mu2, где
U = (u /c)Kr = (u /c)E — энергия деформирования суммарного силового поля,
(5) E = Kr = muc — полная энергия деформирования поля.
Второе — к уравнению баланса энергии дневного вращения частицы:
iU = – imu2/2, где параметр
iU = – (iu /c)Kr = – (iu /c)E определяет величину энергии связи вращающейся частицы с центральным телом в планетной совокупности.
А при подстановке в последнее соотношение параметра (5) приходим к закону глобального тяготения Ньютона в следующих двух формах:
F = – GMm/r2;
тут введена узнаваемая [4] подстановка GM = uiH, где G — постоянная тяготения.
Образование Нашей системы
В соответствии с соотношению (4), осевая магнитная сила iK свободного самовращающегося космического тела тем больше по величине, чем больше момент импульса его iL.
На рис. 5, a происхождение указанной силы представлено в виде затенённой области поля-магнита, ориентированного на протяжении оси самовращения космического тела m1. Разумеется, что такое тело может объединиться с другим m2 (рис.
5, б) либо несколькими вращающимися космическими телами, и это объединение осуществляется благодаря наличию осевых магнитных сил обоюдного притяжения между самовращающимися телами.
В следствии образуется планетная совокупность с неспециализированным магнитным центром самовращения тел, жёсткость силового поля которой определяется суммарным моментом импульса составляющих совокупность планет.
Наряду с этим радиусы r самовращения тел в связанной совокупности значительно уменьшаются, а их окружные скорости u соответственно возрастают так, дабы моменты импульса космических тел при переходе от свободного состояния к связанному оставались неизменными.
В то время, когда в достаточно твёрдое поле появившейся планетной совокупности попадают малые и энергичные (релятивистские) самовращающиеся по малому радиусу свободные частицы мю (рис. 5, б), их скорость может возрасти до предельной, равной скорости света.
Наряду с этим частицы преобразовываются в излучение, образуя со временем в центре планетной совокупности излучающее центральное тело M — звезду.
Так, мы приходим тут к другой модели самозарождающейся планетной Нашей системы: в ней источником судьбы «вечного светила» выясняются не ядерные реакции синтеза, а постоянная подпитка энергией релятивистских космических частиц при наличии замечательной, центрально размешённой магнитной ловушки.
Энергия связи iU тел в планетной совокупности в соответствии с неоклассической теории определяется соотношением, сходным с известным в ОТО выражением для описания перемещения частицы вблизи коллапсара [5]:
(6) – iU/mc2 = {(1 – rg/ir)[1 + (iL /mcir)2







